連立方程式 池の周りを追いつく速さの文章問題を解説 数スタ
旅人算の練習問題と解説 出会い算や追いつき算といった旅人算の練習問題になります。 速さの中では応用問題にあたりますが、1つずつしっかり身に付けましょう。 目次 g6 旅人算 池の周りの出会いと追いつき バージョン ダウンロード 25;
出会い算 池
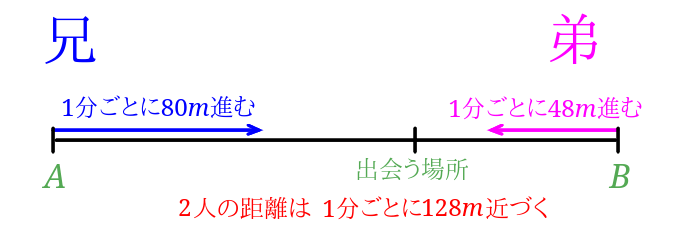
出会い算 池-旅人算 Hello School 算数 旅人算 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 例題1 1400mはなれたA、Bの2地点から、はろ美さんはA地点から分速80mで、すく男君難しく考える必要はありません。 こうしたときは、距離を「1」として計算すればOKです。 池一周の距離を「1」とすると、 9分間で池を一周するひろと君が1分間で進む距離は 1／9 となります。
え こんなに簡単だったの 中学入試の分かりやすい旅人算の解き方 受験ボックス
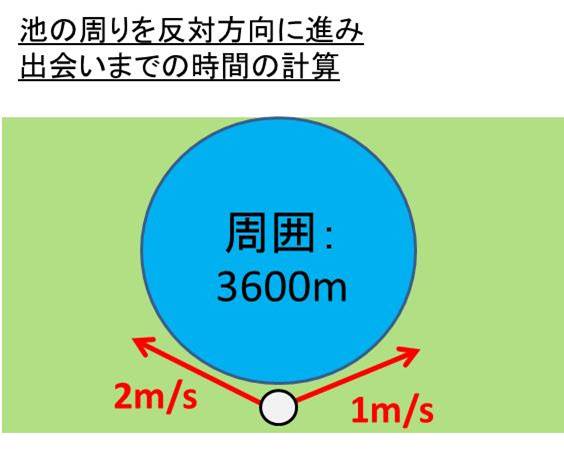
(2)池のまわりを、ゆうこさんが分速mで、ひろみさんが分速 mで 同時に同じ場所から出発し， 反対方向に進んだところ，出発してから、 2人は 分後にはじめて出会いました。池のまわりの長さ何m旅人算⑷ 2回目の出会い・追いこし 6 6 1周270mの池のまわりを、姉は毎分55m、妹は毎分25mで、同時に 同地点を同じ方向に出発し、何周もまわります。 ⑴ 姉が妹をはじめて追いこすのは（ ）★無料の中学メルマガ講座★毎週、問題と動画講義をお届け！ 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料
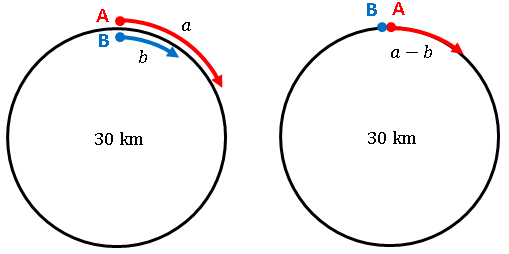
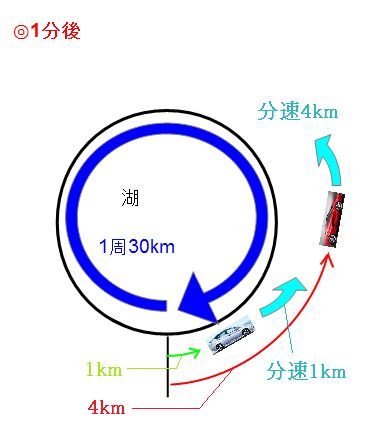
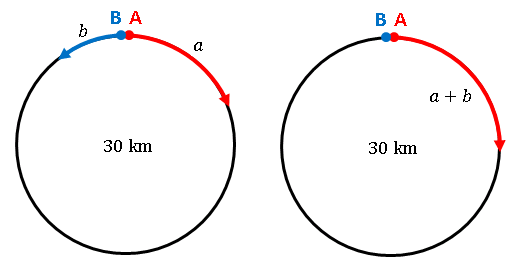
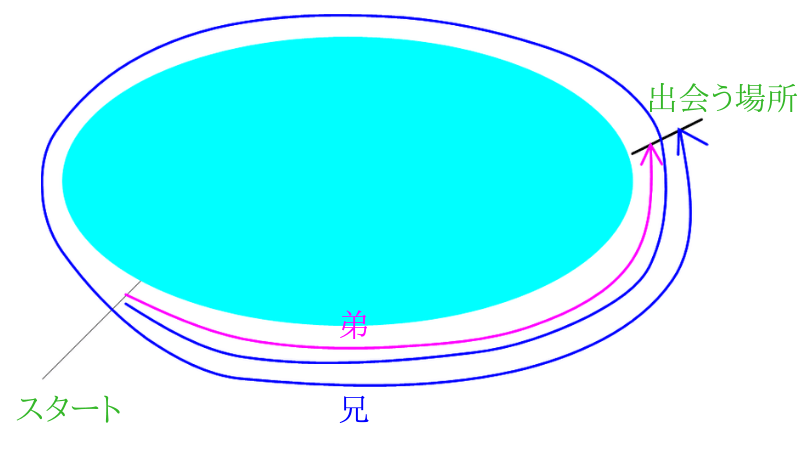
〈例題3〉3人の出会い算 池の周囲をA君とC君は同じ方向に, B君は反対方向に進みます。3人 の速さはA君が毎分 180m, B君は毎分 1m, C君は毎分100mです。 A君とB君が出会ってから 6分たってか旅人算とは、逆向きに進む2人が途中で出会ったり、同じ向きに進む人に出会ったりする、速さの問題です。 主な出題パターンは4つです。 2つの地点から2人が逆向きに進み、途中で出会う 前を進池一周分の、2人の出会いの旅人算が2通り与えられています。 池一周÷（兄の分速＋弟の分速）＝4分 池一周÷（兄の分速－40＋弟の分速－8）＝6分 上の2つの式のカッコの中の部分の比がわかりま
出会い算 池のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |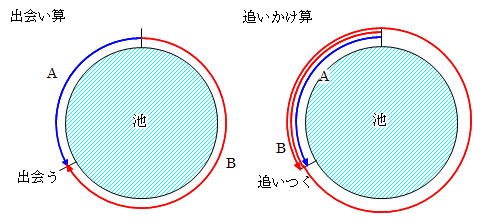
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 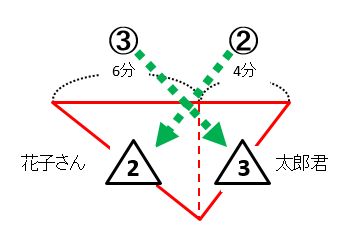 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |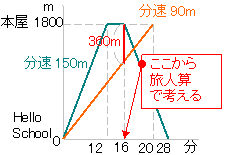
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 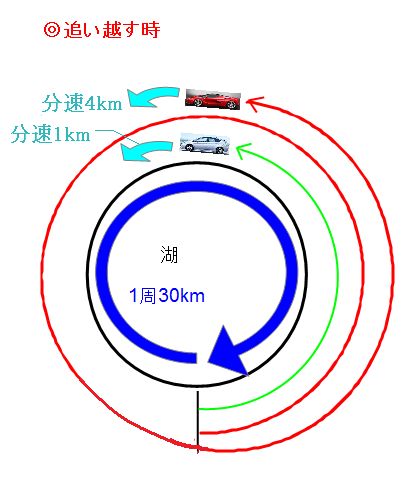 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |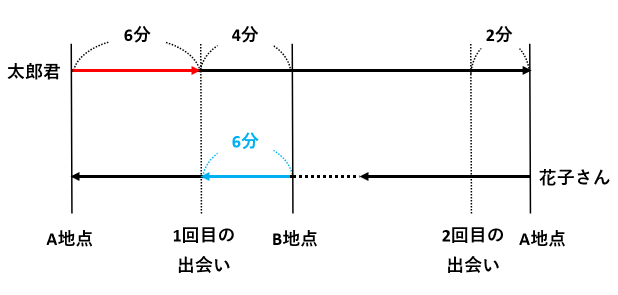
Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 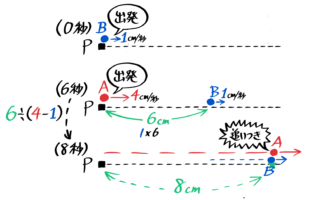 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 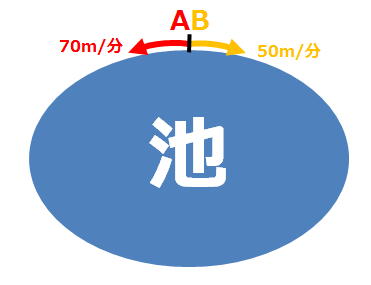 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 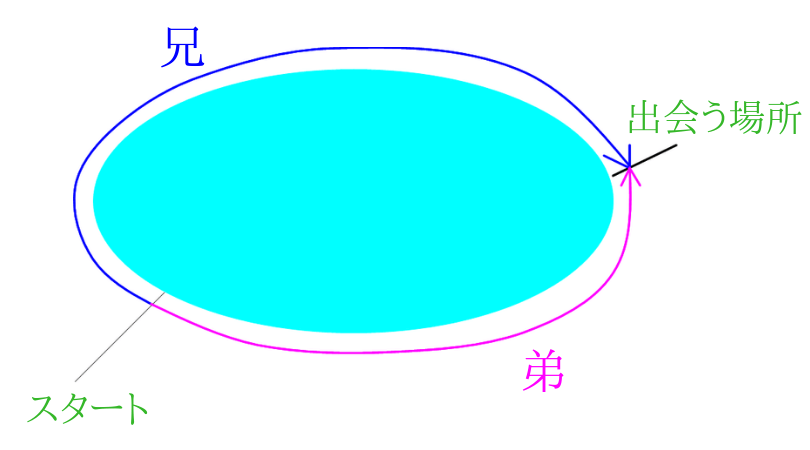 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ | Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 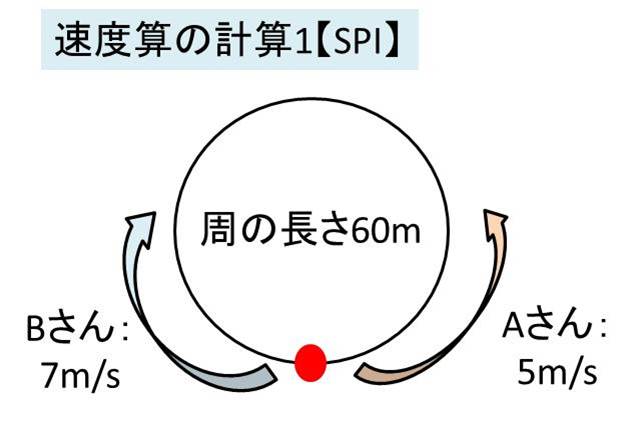 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 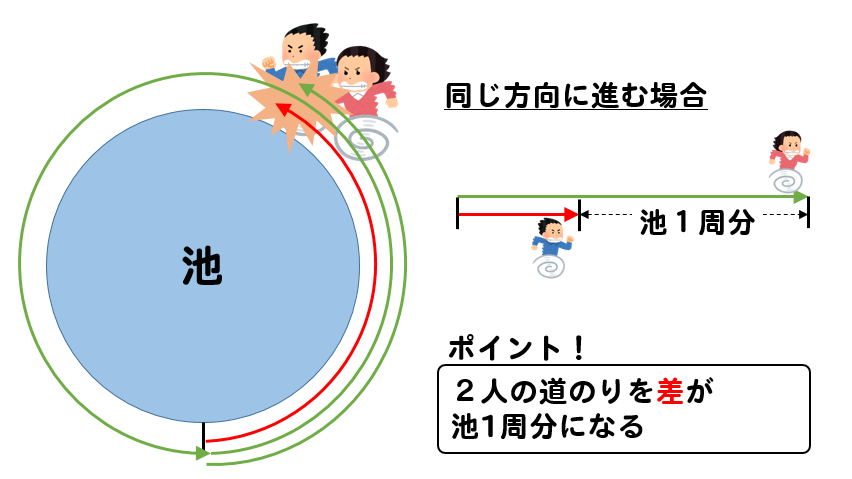 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ | 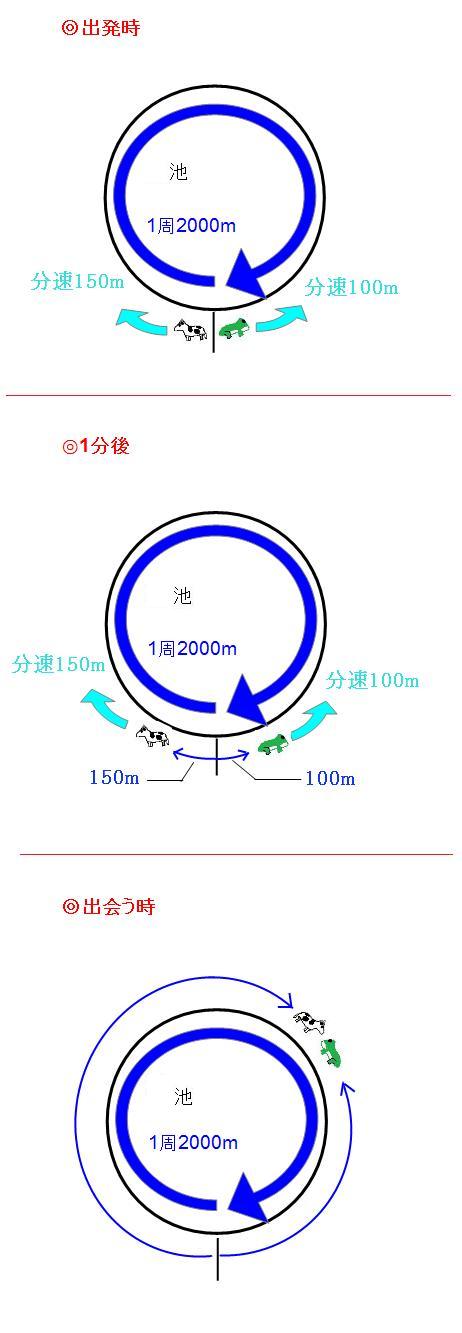 Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
 Math 中学受験 旅人算 発展問題 働きアリ |  Math 中学受験 旅人算 発展問題 働きアリ |
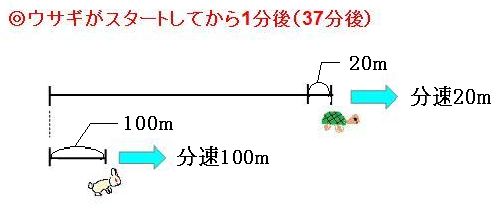
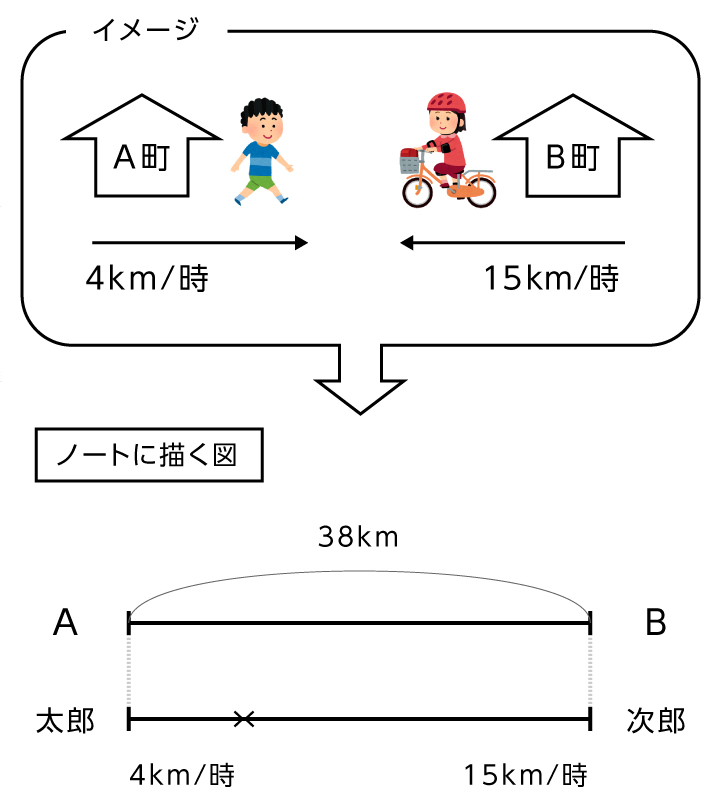
こんにちは、ウチダです。 今日は中学受験算数講座第4回として 「旅人算」 について詳しく見ていきたいと思います。 旅人算の基本は「出会い算」「追いつき算」の $2$ つについてあ 問題の例（1）･･･中1の一次方程式の文章題 ★例題1： 池の周りに1周480mの遊歩道がある。 この道を同じ地点から同時に出発して、Aは毎分65m、Bは毎分55mの速さで歩く。
Incoming Term: 出会い算 池,
0 件のコメント:
コメントを投稿