正十二邊形是指所有邊等長、所有角等角的十二邊形,由十二條相同長度的邊和十二個相同大小的角構成,是一種正多邊形。正十二邊形的內角是 弧度,換算成角度是150度。在施萊夫利符號中用 {} 來表示。正三角形の面積の求め方 そもそも正三角形とは何かというと、 三角形の中で3つ全ての辺が等しいもの を言います。 それを押さえた上で解説を進めます。 上の図のような一辺の長さ の正三角形を考えてみましょう。 三角形の面積の求め方は (底辺)× (高さ)× で求まります。 ここで、正十二角形 定期的な十二角形は、同じ長さの辺と同じ大きさの内角を有する図です。これには、12次の反射対称と回転対称の12本の線があります。正十二角形はシュレーフリ記号{12}で表され、切り捨てられた 六角形t {6}または2回切り捨てられた三角形tt {3として構成できます。
図形 正十二角形の分解 父ちゃんが教えたるっ
正十二角形 面積 求め方
正十二角形 面積 求め方-正 n n 角形の面積 1辺の長さが a a である正 n n 角形の面積 Sn S n は、次の公式で求められる。 Sn = na2 4tan π n S n = n a 2 4 tan 正十二角形の外角は\(360 \div 12=30°\) 正七角形や正十一角形のように $$360 \div 7=5142$$ $$360 \div 11=3272$$ 割り切れ正十二角形の面積の求め方() 連続する二等辺三角形の角度の法則() 重なり部分の面積を考える(麻布中学 13年)() 30゜、60゜、90゜の三角形の面積を求める方




如何求正多边形的面积 7 步骤
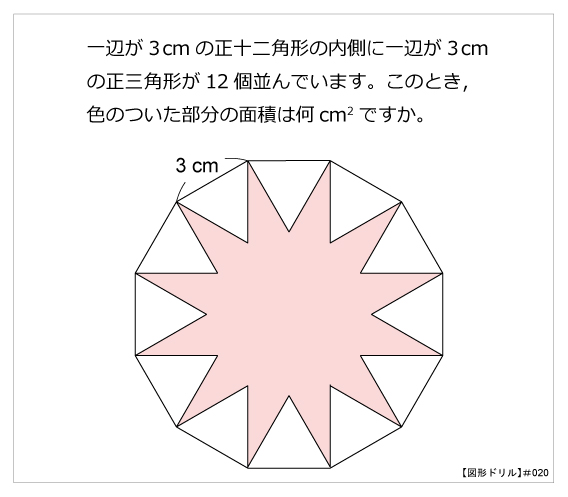
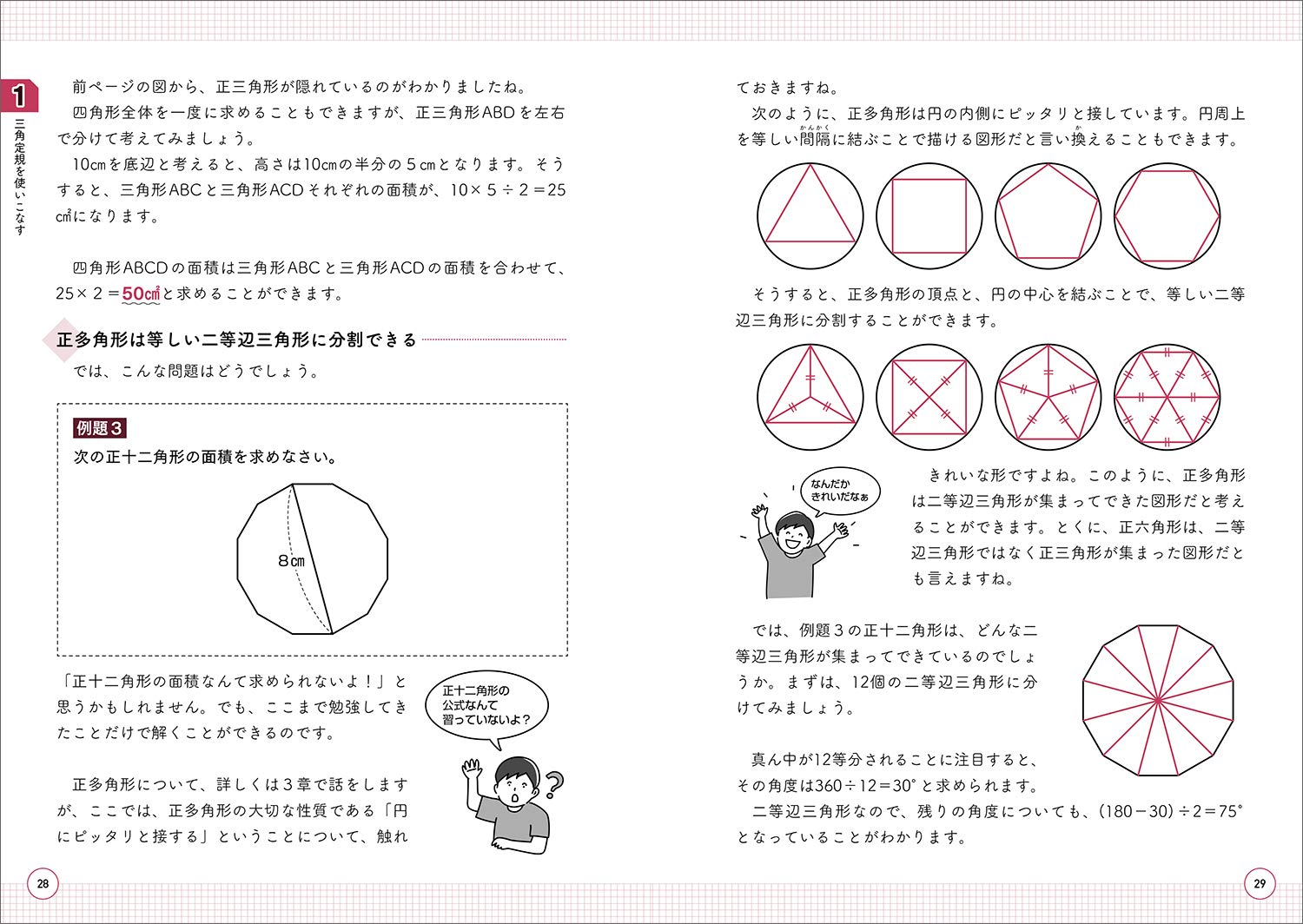
一辺が1cmの正十二角形の内側に、1cmの正三角形が12個並んでいます。 このとき、色のついた部分の面積は何cm 2 ですか。 この問題は、下図のように変形することができ、一辺が1cmの正方形6個分になるので、答えは 6cm 2 。球 半径rの玉の表面積は4πr、体積は4/3πr^3 のとき 半径3の円に内接する正十二角形面積のSを求めよ。 分かるかたがいたらお願いします!(`・ω・´)半径2の円に内接する正十二角形の面積を求めよ。 答 12×(1/2*2sin30°)=12 なのですが、2sin30°はどういった考え方ですか?
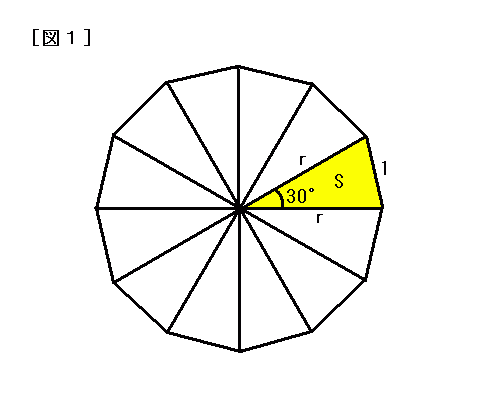
19年 トライアル (算数オリンピック) 19年 30度 5年生 6年生 ジュニア トライアル 正十二角形 算数オリンピック ★★★★★☆(算オリ・灘中受験生レベル) 小学生の知の祭典 算数オリンピック!!円柱の側面積を求めるだけです。 (2) ①おなじみの正十二角形の面積。30度・60度・90度の直角三角形の利用は、受験生には必須の知識です。 (2) ②円柱の容器に入れた水を正十二角柱の容器に入れ替えたときの深さを求める問題。正十二角形においては、 中心角 と 外角 は30 ° で、内角は150°となる。 一辺の長さが a の正十二角形の 面積 Sは
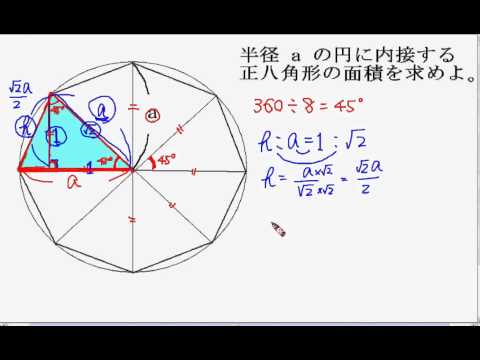
その中に内接する正8角形の面積を考えました。 見通し 正8角形ですから、図の AOBと合同な二等辺三角形が8個あります。 AOBの面積を求めて8倍すれば良いわけです。 解説 AOBの底辺はRで高さはhであるとし、証明 2 (面積を用いた証明) 図 5: 3 <π< 4 の図 半径が r r の円と, それに内接する正十二角形,外接する正方形を図 2 に示した. ここで (正十二角形の面積) < (円の面積) < (正方形の面積) ( 正 十 二 角 形 の 面 積) < ( 円 の 面 積) < ( 正 方 形 の 面 積この立方体を,対角線に垂直な面で切り取るとき,切り口の面積の最大値はいくら になるか。 1 (1) 右図のような補助線を引く。一つの二等辺三角形の面積S は, 4 1 1 sin30 2 S 1 2 o したがって,正十二角形全体の面積はこれを12 倍して3 (2) 右図のようにx を




基測數學 94v2 單選25 六邊形面積 評量專區 均一教育平台




答1474 正十二角形の対角線でできる三角形の面積 ヤドカリの 気ままな数学
正十二角形においては、 中心角 と 外角 は30 ° で、内角は150°となる。 一辺の長さが a の正十二角形の 面積 Sは参考 図1:正十二角形は 個の正方形と 個の正三角形に分割できるから,面積は 図2:図のように, つに分割して並べ替えると を一辺とする正方形になる。正十二角形の面積(中学受験算数 平面図形) 基本レベル Flashによるアニメーション解説が豊富で、解法のイメージ力がつきました。 イメージでわかる中学受験算数 最新の中学受験ドラマや役立つ情報がいっぱい! (ランキング参加中です。 クリック




如何计算六角形的面积 提示 August 21



入試問題に挑戦第4回
正十二角形の対角線の長さ・面積 正十二角形の 辺の長さを ,外接円の半径を ,内接円の半径を とする。 つの辺たとえば に対する弧 の中心角は ,円周角は , 正十二角形の内角は ,外角は である。 A Dodecagon 配点 100 100 点 問題文 半径 a a の円に内接する正十二角形の面積は 3 a 2 3 a 2 であることが知られています。 整数 r r が与えられるので、半径 r r の円に内接する正十二角形の面積を求めて下さい。 制約 1 ≦ r ≦ 100 1 ≦ r ≦ 100 r r は整数で 正十二角形の面積をsとするとき、 この正十二角形が内接する円の面積を求める式を立てよ。 (ただし、円周率は314とする。中学生はπでよい。) 「正十二角形"が"内接する円」とは、 「正十二角形の全ての頂点を通る円」 ということです。



正12 角形 ニスヌーピー壁紙




正多角形の面積 倭算数理研究所
正多角形の面積 sqrt (xx) のように指定してください。 正多角形の1番長い対角線の長さを表示してほしい。 1辺を1としたときと仮定した時でいいので。 非常に役に立った。 立式できても計算に時間が取られていたが、こちらのサイトで瞬時に答えが出た 正十二角形を使う場合 では、ドラマと同じように正12角形でやってみましょう。 同じように、余弦定理を使って式変形していきます。 日常的に計算を行う研究や仕事をしている方だったら、31の2乗の値が961であるということはすぐにでてきます。したがっ正多角形 正三角形 1° 90° 72° 60° 360° 7 45° 正六角形 正七角形 正八角形 正六角形 正七角形 正八角形 正四角形(正方形) 正五角形 正三角形 正四角形 正五角形 (正方形) 小学算数 5年3-2① さらにくわしくお知りになりたい場合 教授用資料 啓林館教師用




正12 角形 ニスヌーピー壁紙



正十二角形の面積は 大宮開成中学 2010年 どう解く 中学受験算数
大至急‼ 正十二角形の3頂点を結んで出来る三角形を考える。 (1)三角形は全部でいくつあるか。 (2)もとの正十二角形と1辺のみを共有する三角形はいくつあるか。 (3)もとの正十二角形と辺 を共有しない三角形はいくつあるか。 (4)正三角形はいくつあるか。正八角形の中に二等辺三角形が8つ分できてることに気が付きますね。 なので、 二等辺三角形の面積を求めて、それを8つ分にする。 という考え方で正八角形の面積を求めていきます。 中心の360°を8等分していることから5年算数 円と正多角形 2 子どもの学習支援 by いっちに算数 スマホ版 前のページにもどる ↑正多角形の書き方(アニメ) 教え方3 教え方3-① 円周と直径の意味を教え、円周の長さと直径の長さの関係を調べさせ、円周率を理解させます。




おもしろ算数問題 シンプルで 複雑な計算も不要な正十二角形の問題 Youtube



十二边形 维基百科 自由的百科全书
E 7 i y l F ӂ ̂ 炢 j } ̂悤 ɐ \ p ` ̕ӂ̂Ƃ ɁA O p ` ܂ B i F ̐ O p ` P Q j正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法 次は内角の和から1つ分の大きさを求める方法です。 まず、多角形の内角の和は $$\LARGE{180 \times (n2)}$$ で求めることができましたね。 正三角形の内角の和であれば (3) 正十二角形のすべての頂点から対角線を引くと、 \(12\) 個の合同な二等辺三角形ができる。 この三角形の頂角は \(360^\circ \div 12 = 30^\circ\)




如何查找正多边形的面积 7个步骤 带有图片 百科全书 21




正多边形二十角形内角petrie多边形png图片素材免费下载 图片编号 Png素材网
正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の円に外接する正多角形 底面から柱へのステーの長さを算出させていただきました。 使い易いです。 ありがとうございました。 aの計算式ってあってますでしょうか? 計算自体はあってるのですが、式が違う気がするのですが 関数電卓で計算すると問題154 正十二角形の問題 の解は 166 cm です。 解き方 小円の半径を r とすると、内接する12角形を構成する三角形 1 個の面積は 1/2 x r 2 x sin (2π/12) = 1/2 x r 2 x 1/2 = 1/4 x r 2 同様に大円では 1/4 x (r 2) 2 水色の部分の面積は、両者の差の 12 倍であるから 1




十二边形 维基百科 自由的百科全书



図形 正十二角形の分解 父ちゃんが教えたるっ
考え方と解答 次の図のように,正十二角形を12等分して $\sankaku{OAB}$ の面積を考える。 $\sankaku{OAB}$ の面積を求めるために,OAの長さを求める。 $\kaku{AOB}=30\Deg$ であることが分かるから,余弦定理でOAを求めよう。 $\text{OA}=r$ とするとる正N 角形の1辺の長さを2aとすると,pN = (N 2a)=2 = Naである.一方, 図3において,OA = 1, BC = aであるから,三角形OAB の面積は, 1 2 1 a = 1 2 a である.したがって, s2N = (2N) 1 2 a) = Na = pN (1) である.すなわち,正2N 角形の面積s2N は,正N 角形の周の長さの半分pN に等 しい.したがって,N !P193 千思万考 正十二角形の頂点と三角形の面積 2 (1) OAD 底辺1,高さ1の直角二等辺三角形 (2) OHJ 各辺が1の正三角形 面積は DM= 1 2 3



正12 角形 ニスヌーピー壁紙



中学数学 面積に関する質問です 1辺が2cmの正六角形を2つ重ねて Yahoo 知恵袋



入試問題に挑戦第4回




直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com



12 Jpg




正十二角形の図形問題 仙台市立中等教育学校 年 恋する中高一貫校 適性検査 徹底攻略




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト



三平方の定理の応用はこれで決まり正十二角形編その2 返事はハイ



六边形 Wikiwand




如何计算六角形的面积 提示 August 21



図形 正十二角形の分解 父ちゃんが教えたるっ
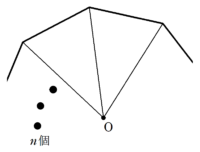



正多角形の面積の公式 一般化 Fukusukeの数学めも




算数 53 正十二角形の面積 城北 平面図形 Youtube



六角形棱镜正多边形六角形瓦形png图片素材免费下载 图片编号 Png素材网




如何求正多边形的面积 Find The Area Of Regular Polygons Tl80互动问答网
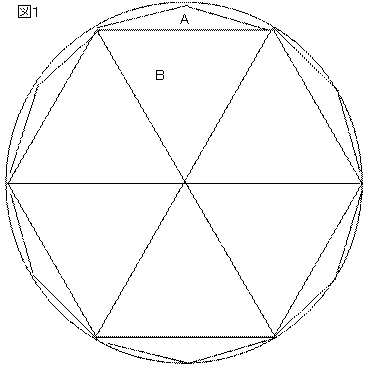



問題187 正十二角形の秘密




十二边形 维基百科 自由的百科全书




六角形面積公式正六邊形 Utvos




十二角正多边形八角形png图片素材免费下载 图片编号 Png素材网



六角形面积怎么计算 西瓜视频搜索




4种方法来求六边形面积



図形 正十二角形の分解 父ちゃんが教えたるっ



六角形面积怎么计算 西瓜视频搜索




六角形面積公式正六邊形 Utvos



中3数学 正八角形の面積 Youtube
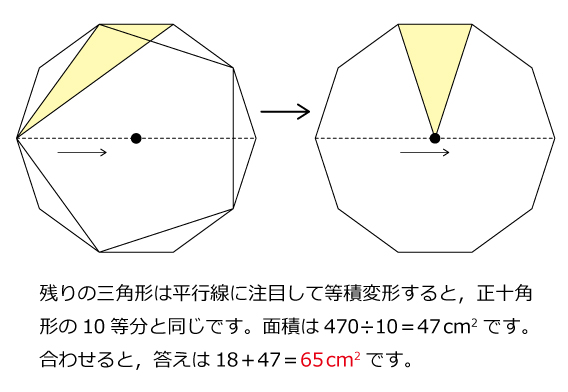



今年の1問 年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦




一般 正三角形的高與面積 Youtube




4种方法来求六边形面积




六角非角形十二角形png图片素材免费下载 图片编号 Png素材网




如何求正多边形的面积 7 步骤



正12 角形 ニスヌーピー壁紙
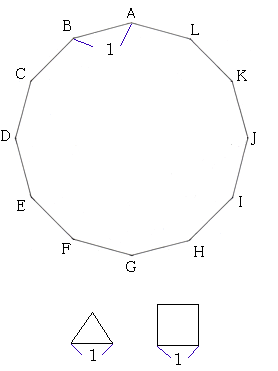



問題187 正十二角形の秘密



正12 角形 ニスヌーピー壁紙




十二边形 维基百科 自由的百科全书




如何求正多边形的面积 7 步骤




算数 116 正十二角形の面積を求める 香蘭 平面図形 Youtube
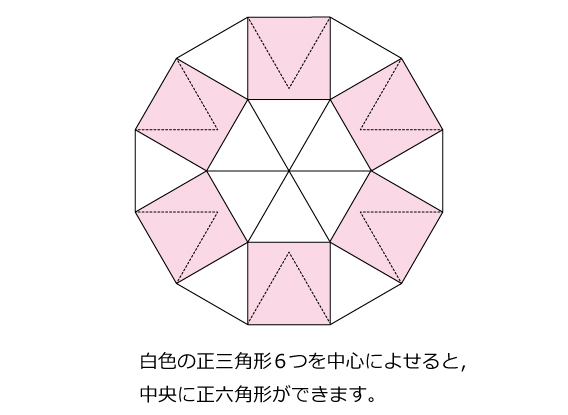



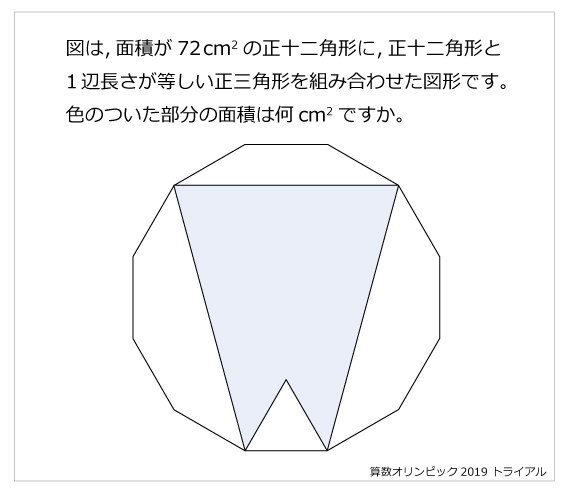
図形ドリル 第問 正十ニ角形と正三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




六边形 维基百科 自由的百科全书




ハは肺魚のハ 跡地 直径10cmの正十二角柱型プリンの体積の求め方



Q Tbn And9gcr6br Oxol4soj8jhaap6e5yoavx9 Cepch0ccusgm Usqp Cau



入試問題に挑戦第4回
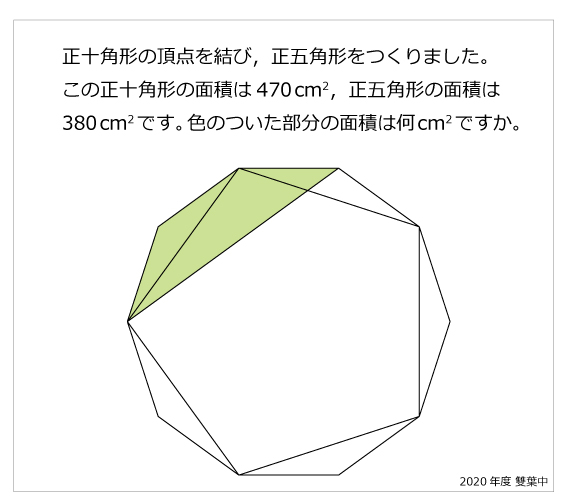



今年の1問 年雙葉中 正五角形と正十角形 算数星人のweb問題集 中学受験算数の問題に挑戦




面白い数学の問題 算数オリンピックからの挑戦 正十二角形の謎を解く そらの暇つぶしch



図形 正十二角形の分解 父ちゃんが教えたるっ



正12角形の面積 半径2の円に内接する正12角形の面積を求 Yahoo 知恵袋




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月
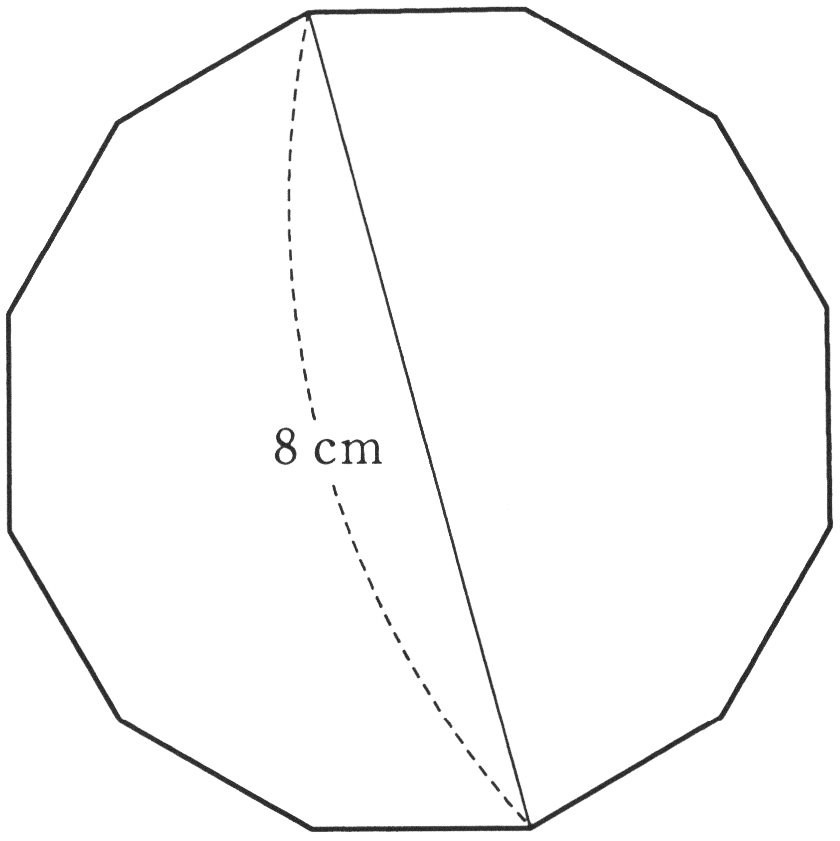



正十二角形の面積 城北19 ジーニアス 中学受験専門塾



六角形面积怎么计算 西瓜视频搜索




六角形面積公式正六邊形面積公式 百度知道翻譯此網頁 Juliech
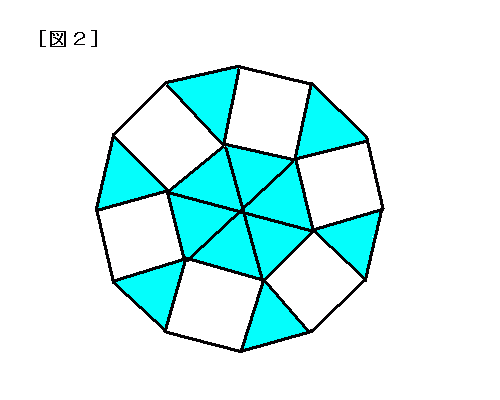



問題187 正十二角形の秘密



半径2 の円に内接する正十二角形の面積を教えて下さい 内 Yahoo 知恵袋




正六角形三角形小學數學三角形的特性知識點大全 Vnfp




六角形面積公式正六邊形 Utvos




怎么计算六角形的对角线长 院勾问答




魔术六角形内角 六边形png图片素材免费下载 图片编号 Png素材网




如何求正多边形的面积 7 步骤



正12 角形 正12角形対角線



1



8角形怎么画 西瓜视频搜索




六角形面積公式正六邊形 Utvos




おもしろ算数問題 シンプルで 複雑な計算も不要な正十二角形の問題 Youtube



Q Tbn And9gcsddmpkoyaml V14rabsbpkwb5qihiuzm9uzlifiqxark4gsgq0 Usqp Cau



六角形面积怎么计算 西瓜视频搜索
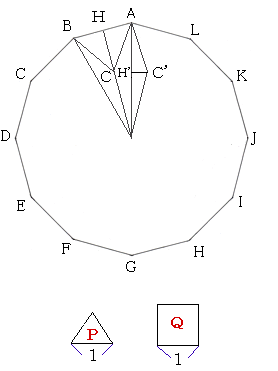



問題187 正十二角形の秘密




半径2の円に内接する正十二角形の面積を求めよ 答 Clear



1



図は一辺が2cmの正六角形と6つの辺が正六角形の周上にある正十二角形 Yahoo 知恵袋
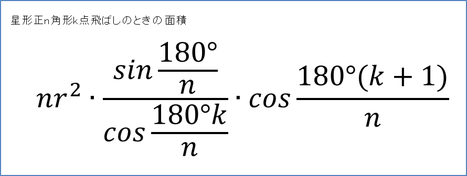



つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




4种方法来求六边形面积
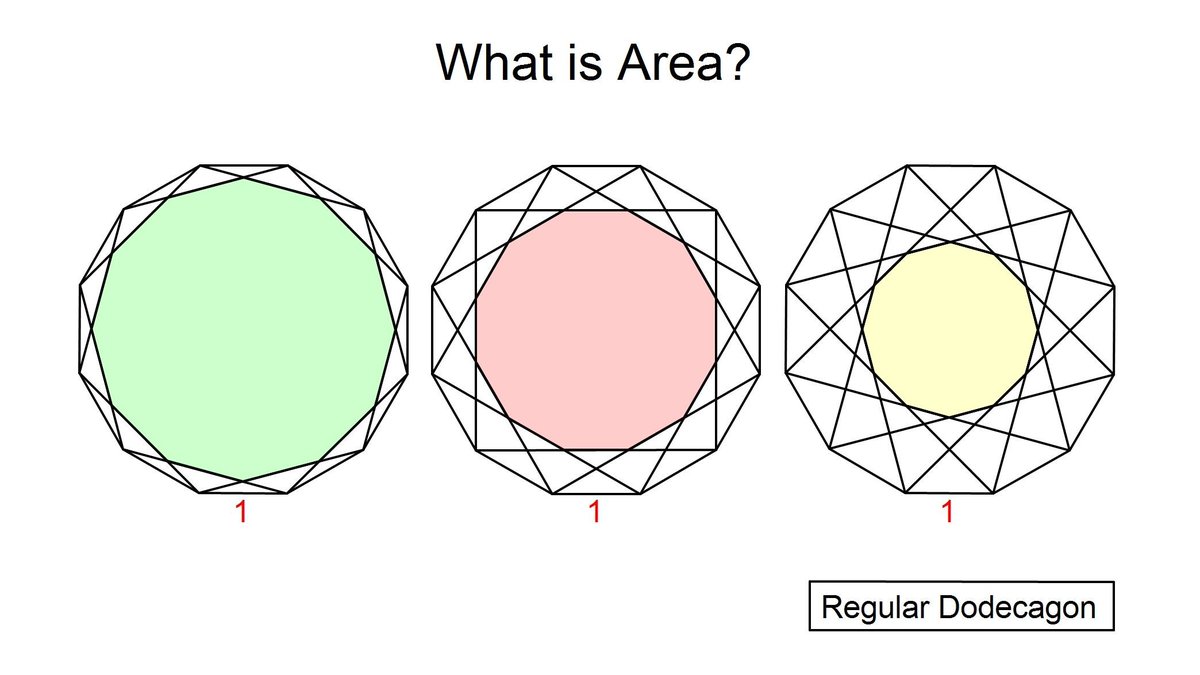



ポテト一郎 正十二角形パズル 色のついた正十二角形の面積は
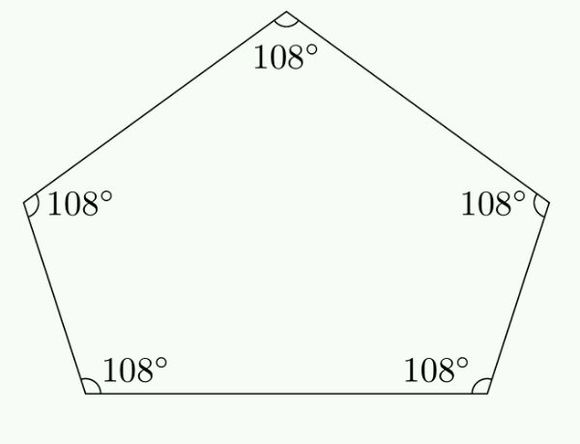



正五邊形 定義 面積公式推導 內切圓半徑 構造 物理方法 畫法 常規畫法 尺規作圖 中文百科全書



图说正十二边形的面积




兩個小學生的12邊形燒腦題 每日頭條



正十二角形の面積の求め方 算数解法の極意




十二边形 Wikiwand



正12 角形 ニスヌーピー壁紙




十二边形 维基百科 自由的百科全书




如何计算六角形的面积 提示 August 21



12角形の面積



図形 正十二角形の分解 父ちゃんが教えたるっ
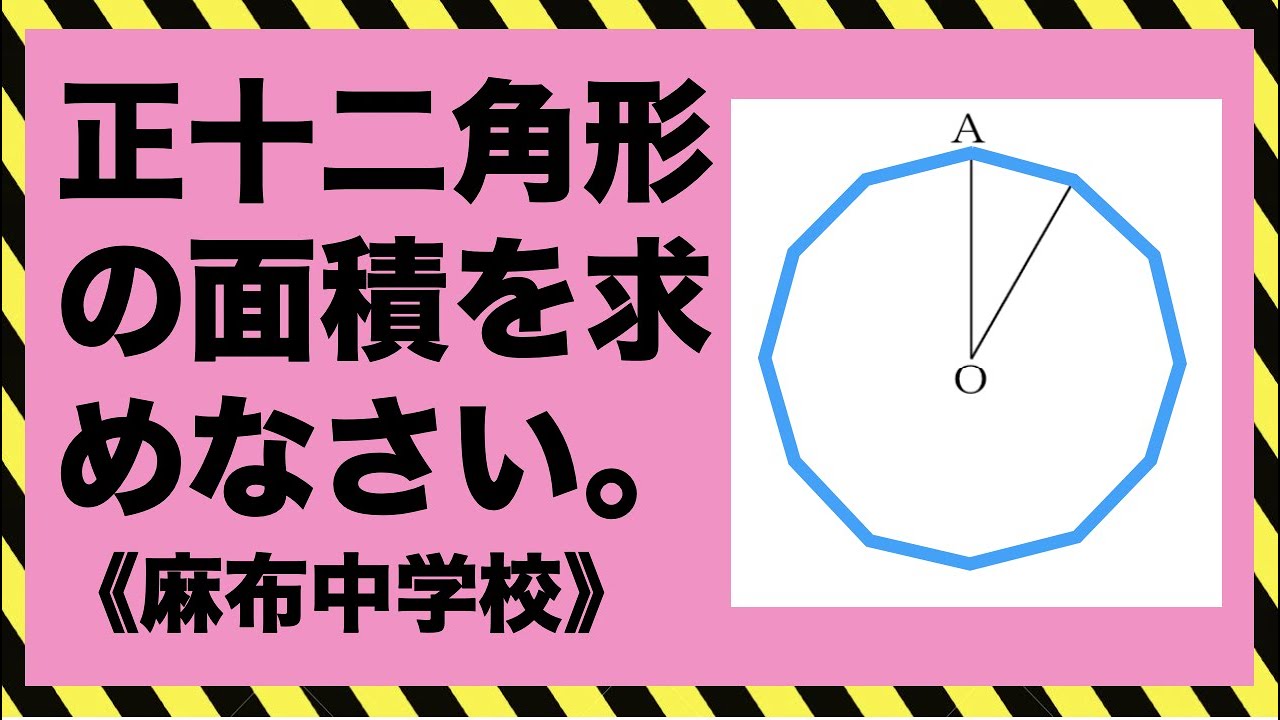



麻布中学校 算数 正十二角形 面積 図形問題 中学受験算数 勉強 Youtube スタディチューブ




答1474 正十二角形の対角線でできる三角形の面積 ヤドカリの 気ままな数学




正多边形 维基百科 自由的百科全书




正六角形的面積 英 Khan Videos 均一教育平台




如何求正多边形的面积 Find The Area Of Regular Polygons Tl80互动问答网



問題187 正十二角形の秘密



合格する算数の授業 図形編 中学受験 だから そうなのか とガツンとわかる Amazon Com Books




兩個小學生的12邊形燒腦題 每日頭條



正十二角形 算数星人のweb問題集 中学受験算数の問題に挑戦




正十二角形の面積 スクールプレゼンター教材共有サイト スクプレ道場



0 件のコメント:
コメントを投稿