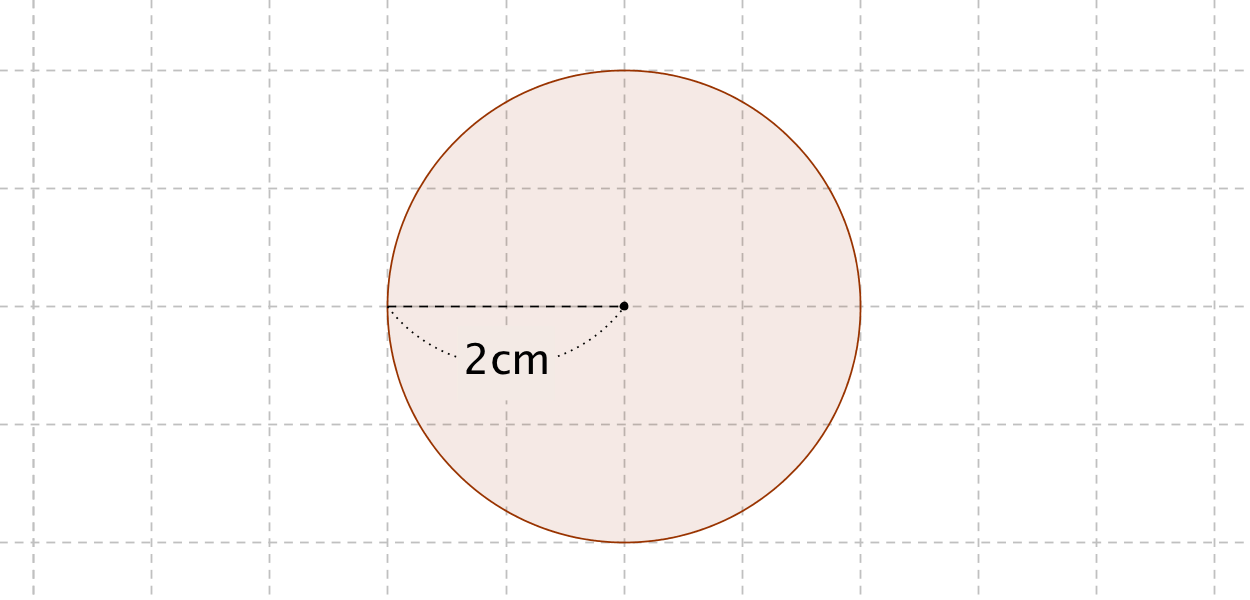
1分子の表面積がa 0で、液体が表面積Aだけ新 しい表面を作るのに必要なエネルギーは 2 2 b bAA s s AA Z E Z E 00 2 es b s b AA EEE ZZ a :表面張力 次元 mNm1=「mJm2 表面の分子は内部に比べて過 剰なエネルギーをもっている 計算例:クロロホルムまた,三角形の面積の公式から, S = 1 2 b c sin A S=\dfrac{1}{2}bc\sin A S = 2 1 b c sin A 以上の2式から sin A \sin A sin A を消去して整理すると求める公式を得る。 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい
小6算数 円の面積 指導アイデア みんなの教育技術
縁の面積の公式
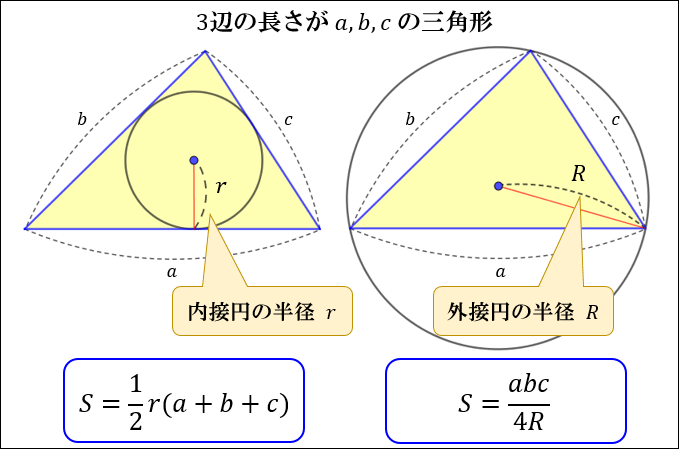
縁の面積の公式-円の面積 ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ)翼面積 翼平面形の面積。投影面積とも。翼を平面に投影したときの最大投影面積を翼面積とする。胴体と重なる部分も含めて考える。数式では s で表されることが多い。 アスペクト比 一般には長方形の縦と横の長さの比のこと。



実践記録算数5年
松江市:総合メニュー コロナワクチン接種のスケジュールをお知らせします (21年04月09日) 市内での新型コロナウイルス感染症の発生状況について更新しました (21年05月26日) 松江市新庁舎の整備について更新しました (21年05月10日) 松江のて、三角形 の面積 の公式 を考える 。 (表)公式 を用いて 三角形 の面積 を求めるこ とができる 。 (知)三角形 の面積 の求め方を理解 している 三 角 形 の 面 積 の 求 め 方 1 (本 時) ・高さが 三角形 の外にある 場合 でも 、三角形 の面積 の公式 が適用 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいの
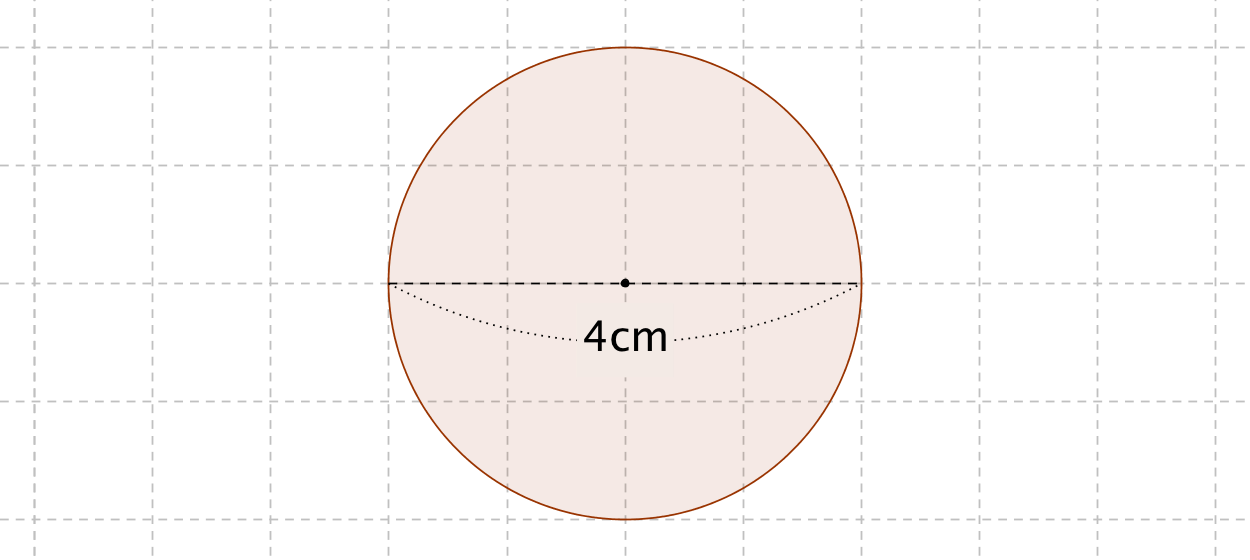
この面積は翼の断面形あるいは平面形とともに,飛行機の性能を左右する非常に重要な要素の一つである。 おもな旅客機の翼面積は, 980ft 2 (約91m 2 ) 5,500ft 2 (約511m 2 ) 777 4,607ft 2 (約428m 2 ) エアバスA310 2,357ft 2 (約219m 2 )円の面積=半径×半径×3.14 教え方4 教え方 4 練習問題を通して、円の面積の勉強のおさらいをさせます。 最後に この勉強では、円の面積を求める公式を使って、円の面積やいろいろな形の面積を求めることをねらいとしています。スポンサーリンク \ 円周 = 直径 \times 円周率 \ 練習問題① 直径が 4cm の円周を求めてみましょう。ただし円周率は 314 とします。 円周を求める公式は \ 円周 = 直径 \times 円周
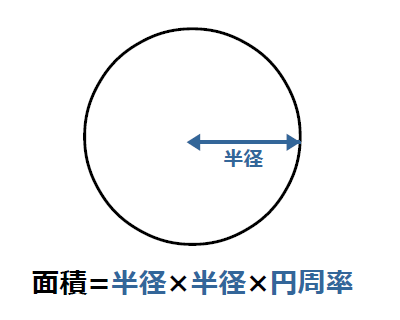
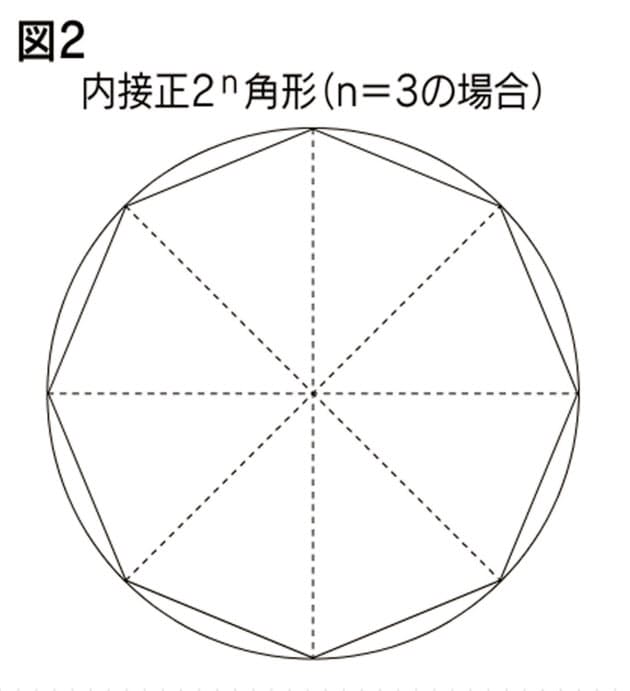
これは大事な公式ですからしっかりと覚えておきましょう。 円の面積の求め方は、 (円の面積) = (半径) × (半径) × (円周率π) ですね。 ここまでわかれば、準備完了です。 ・底面の円の面積は 3×3×π=9π㎡ ・高さは 8cm よって、求める円柱の この記事ではこんなことを紹介しています 「円の面積の公式である\\(S=\\pi r^2\\)が、なぜそのような形で書けるか」 ここではその理由を、図形を使って視覚的に納得できる説明を紹介します。 証明には小学校の算数の知識までしか使わないので、小学生に理由を聞かれたときにも使えま円の面積の公式を 導きだそうとしてい る。 3 単元構成(全5時間) 時 主な学習活動 つなぐ既習事項と教師の支援 1 円に内接する正方形と外接す 5年 円と正多角形 る正方形の面積と比べること 円に内接する正六角形と円に外接する正方形を利用



円の面積 円周の求め方 公式 小学生 中学生の勉強



250枚 至急 葉っぱ形の図形の面積について質問です Yahoo 知恵袋
円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるのだろうか。 様々な証明方法があるが、まず三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)積分法(せきぶんほう、英 integral calculus )は、微分法と共に微分積分学で対を成す主要な分野である。 実数直線上の区間 a, b 上で定義される実変数 x の関数 f の定積分 (独 bestimmtes Integral, 英 definite integral, 仏 intégrale définie) ()は、略式的に言えば f のグラフと x軸、および x = a と



円周の公式 算数の公式



小6算数 円の面積 指導アイデア 2 みんなの教育技術
2 例題1次のH 形断面に曲げモーメントM=80kNm=80×106Nmm が作用するときの縁応力度およびフ ランジとウェブの接合部の応力度を求めよ. H 解 2 6 6 2 6 6 1 4 3 3 3 3 5 1249N/mm 10 80 10 500 11N/mm 10V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jinA=面積 a=面積 a=面積 もし とすれば a=面積 a=面積 もし とすれば a=面積 p=楕円の周囲 a=πab 、pを求める近似式 a=面積 a=面積bcd a=面積 なお点線に示すよう二つの三角形となし 各々の面積を計算しその和をもって 不平行四辺形の面積を算出してもよい =弧の




実践記録算数5年



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
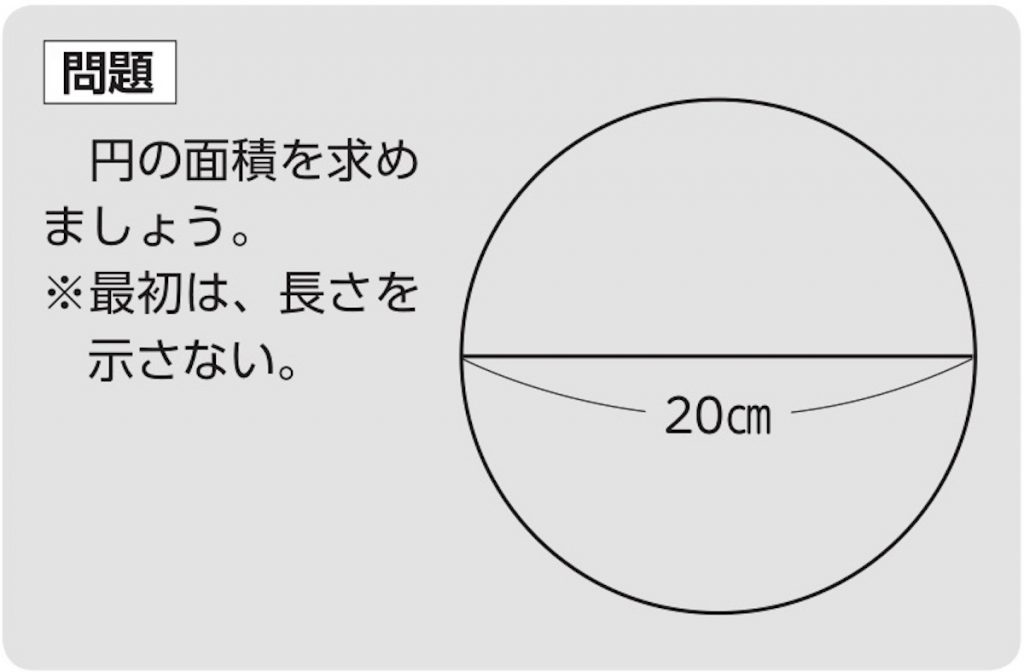
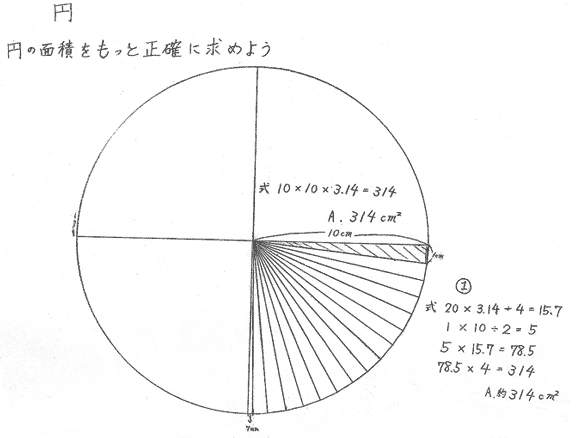
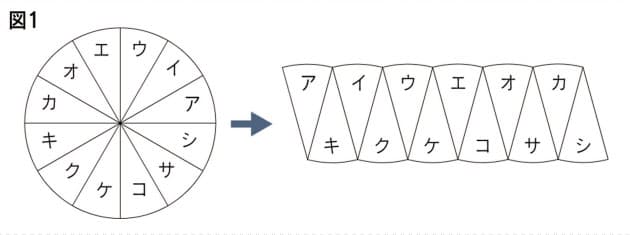
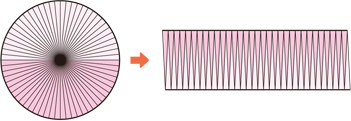
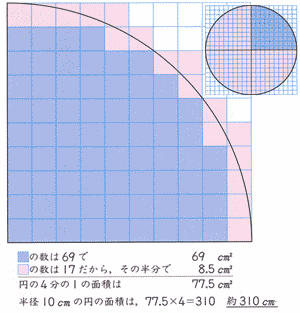
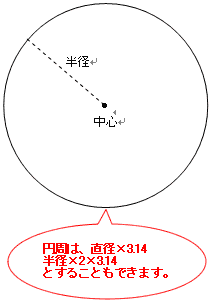
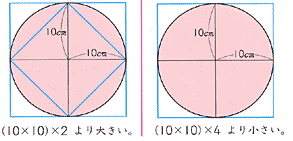
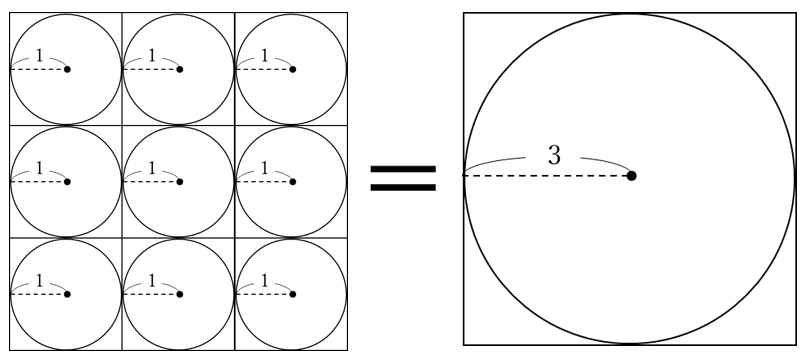
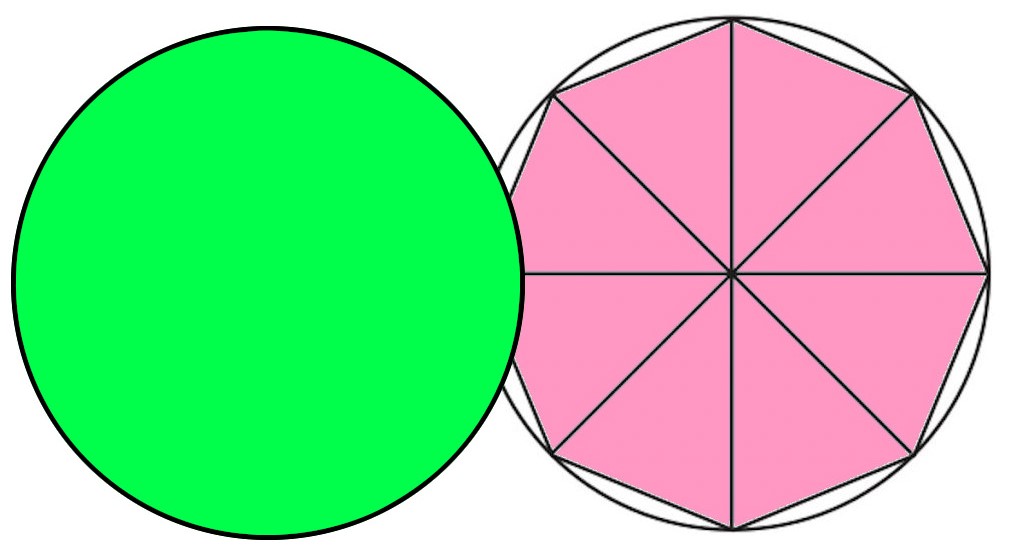
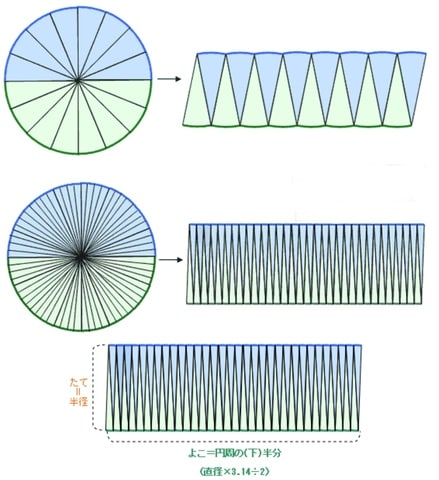
中学数学「円の面積の求め方」の公式を1発で覚えてしまう裏技 中2数学 玉を取り出すときの確率を4秒で計算できる公式完成時に引張応力を受ける両縁支持板が、架設時の 一時的な圧縮応力を受ける場合、不経済な設計を避 けるため、最小板厚制限を緩和。 387 b, t b t 210,000 40π 12(1μ) E σ t b 0109σ γ 05σ σ, 07 R R 05 σ σ 2 2 2 y 2 Y Y cal 2 Y cr < = = = < 応力勾配による係数円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか




円の面積の求め方 公式と計算例



子供に説明できる 円の面積の公式 の証明 Nikkei Style
円の半径とは、円の中心から円周上の任意の点を結んだ線の長さです。 半径を最も簡単に求める方法は直径を2で割ることです。 直径がわからなくても、円周 ( C = 2 π r {\displaystyle C=2\pi r} )や円の面積 ( A = π r 2 {\displaystyle A=\pi r^ {2}} )など他の値が与えられる(圧縮縁から04x)ので、終局曲げモーメントMuも簡易に計算できる。 T s A s f y b d h x cu' s C c' T s z 085f c' 断面図ひずみ分布 応力分布 085f ' 08x C c' T s d04x 等価応力ブロック ②一方、引張鉄筋の降伏を仮定すると、引張合力は、 ここではこんなことを紹介しています↓ 円の面積の公式はなぜ「\\(π\\)×\\(r\\)×\\(r\\)」と表現できるのでしょうか? ここではそんな疑問に対して、図形を使った簡単な公式のイメージ方法を紹介します。 先に言っておくと、ここで紹介する方法は円の面積の厳密な証明方法ではありません



円の面積の公式 算数の公式




円の面積 その2 家庭学習レシピ
円の直径D=8cmです。よって円の面積Aは、 です(π=314で計算)。 円の直径から面積に変換する公式は、数学だけでなく物理や工学でも使います。必ず覚えておきましょう。直径、円の面積の詳細は下記が参考になります。 φと直径の関係は? 小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分 単純に、円の面積を中心角 2π 2 π ( 360∘ 360 ∘ )の扇形と見て、面積は中心角の大きさに比例するので、扇形は円の面積の θ 2π θ 2 π 倍である。 よって、扇形の面積を A(r) = 1 2 r2θ A (r) = 1 2 r 2 θ と求めても良いでしょう。




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



円の面積 算数用語集
グリーンの公式 領域D を細かい正方形に分割して、縁に沿った回転量を足 し合わせると、隣り合った正方形の境界上は打ち消し合っ て、領域の縁に沿った和だけが残る。 分割を細かくしてh → 0 の極限を取ると以下のグリーンの定 理が得られる:Z C Fdr 公式の証明2 内接円の半径の公式を証明する方法は他にもあります。証明1に比べて計算も大変で筋が悪いですが, 全てを a, b, c a,b,c a, b, c で表す という方針でも証明できます。 @ ̑̐ρE \ ʐς̌ ̂ Ƃ ؖ ́C Z wIII i 3 j Ŕ ϕ p čs 邪 C ܂łɂ o ꂷ ʂ C ̑̐ρE \ ʐς̌ ͏ w Z ̓ Ɋo Ă Ƃ悢 D m ̑̐ρn



6年算数 円の面積 2 わかる教え方




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
円の面積の求め方 公式と計算例 Scipursuit 面積の求め方 円 円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314 中学生以上では、文字を使って次のように書きます。 S = πr2 S = π r 2 半径 r の円谷(山)の数を数えるのが面倒な場合は凸凹に対して垂直の長さを測り、一谷の幅0mmで割れば、谷の数も分かるので面積を求めることが可能です。 仮に凸凹に対して垂直の長さが10mだった場合 10m×1000=mm ÷0×2= メーカーや製品によって高さやを用いても,直ちに示せる. =r より x 2 y 2 =r 2 ※ 点 P が座標軸上(通俗的に言えば,赤道上または北極,南極の場所)にあるとき,直角三角形にならないが,たとえば x 軸上の点 (r , 0) についても, r 2 0 2 =r 2 が成り立つ.このように,座標軸上の点については直角三角形はできないが,この
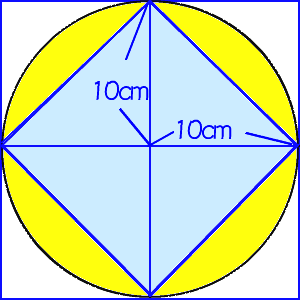



6年算数 円の面積 1 アニメでわかる教え方
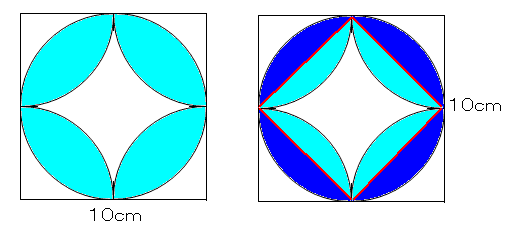



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素
No011 弓形の面積と円弧の長さ A:弓形の面積 m 2 ,l:弓形の円弧の長さ m,r:弓形の半径 m,θ:弓形の角度 °円の面積の公式 円の面積は 『半径×半径×円周率』 で計算できます。 たとえば以下のような問題の場合。 例題 半径 2cm 2 c m の円の面積を求めよ。 答えはこのように求めることができます。 2 ×2× 314=1256(cm2) 2 × 2 × 314 = 1256 ( c m 2) つづいて、なぜ円AとCに囲まれた図形は、図Bの青い部分と黄色い部分の2つ。 そのうち、 x 軸よりも上にあるもの、つまり青い部分の面積を問われている。 図Bの青い部分は y 軸に関して対称なので、 y 軸より右の部分の面積を求めて、2倍する方針で解く。 ところが、数
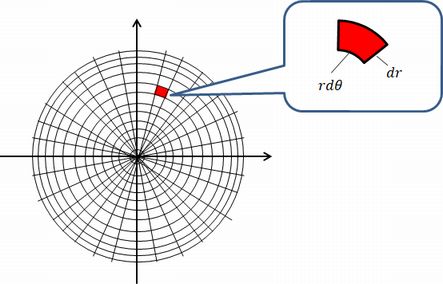



極座標で円の面積を求める方法の補足 おにノート おーにしの物理 数学ノート




円の面積 円周の求め方 公式 小学生 中学生の勉強
求積公式(平面) a=面積 正方形 長方形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 円 a=面積 円分 欠 円 環 形 扇 形 角 縁 a=面積三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度
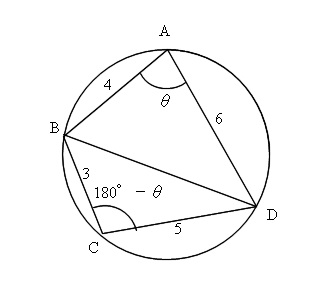



円に内接する四角形の面積の求め方と定理の使い方




円の面積 算数用語集



円の面積を 一般的に知られている公式を使わずに算出する方法を教えてくれませんか Quora




扇形の面積の求め方 公式と計算例




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
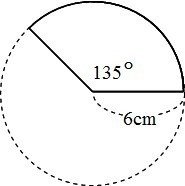



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




小6算数 円の面積 指導アイデア みんなの教育技術




微分でつなげる円や球の公式 すうがくブログ 式変形ch



6年算数 円の面積 2 わかる教え方



円の面積と公式 面積計算機
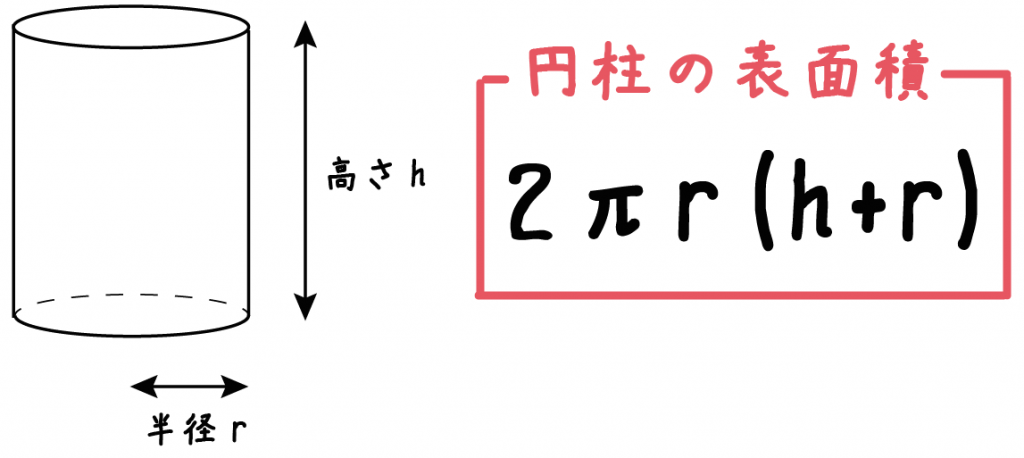



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
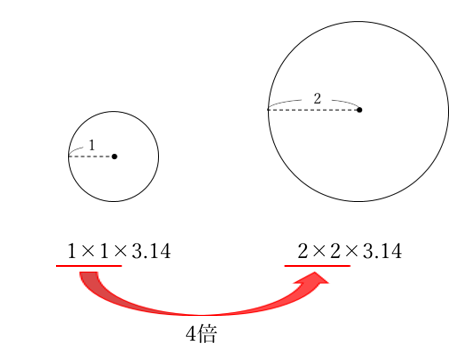



円の相似を利用した面積の計算 中学受験プロ講師ブログ



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau



実践記録算数5年




小6 算数 小6 2 円の面積 応用編 Youtube
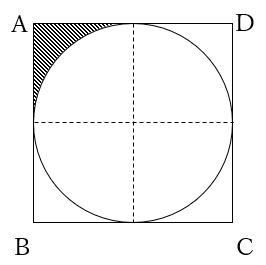



半径の分からない円の面積 中学受験プロ講師ブログ




円の面積 円周の求め方 公式 小学生 中学生の勉強




円周の求め方と円の面積について アタリマエ



円の面積計算 ゆるゆるプログラミング




アルゴリズム 2つの円の重なった面積 Teratail




円柱の表面積と体積を求める公式 具体例で学ぶ数学



面積を求める
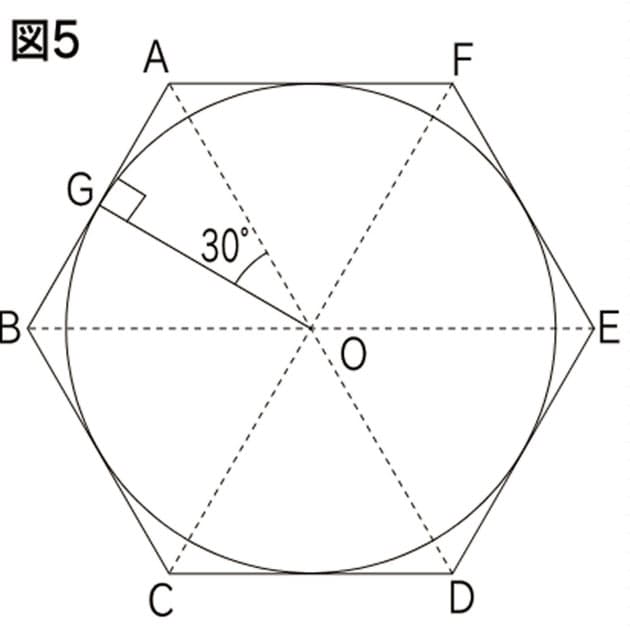



子供に説明できる 円の面積の公式 の証明 Nikkei Style




6年算数 円の面積 1 アニメでわかる教え方
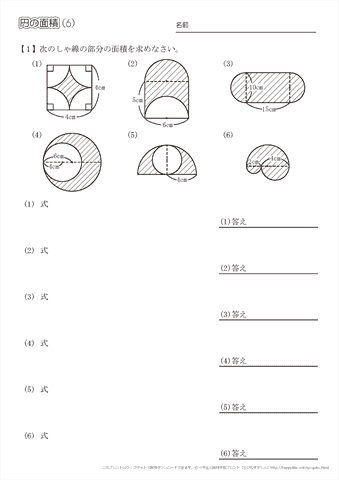



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
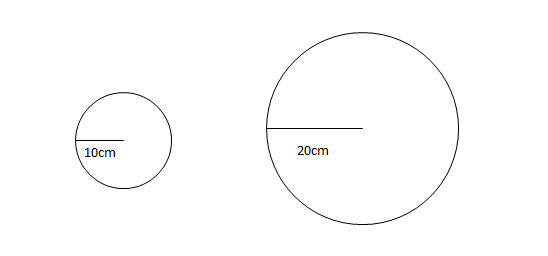



小学算数 円の半径と面積と円周の関係を理解しよう 偏差値40プログラマー



1
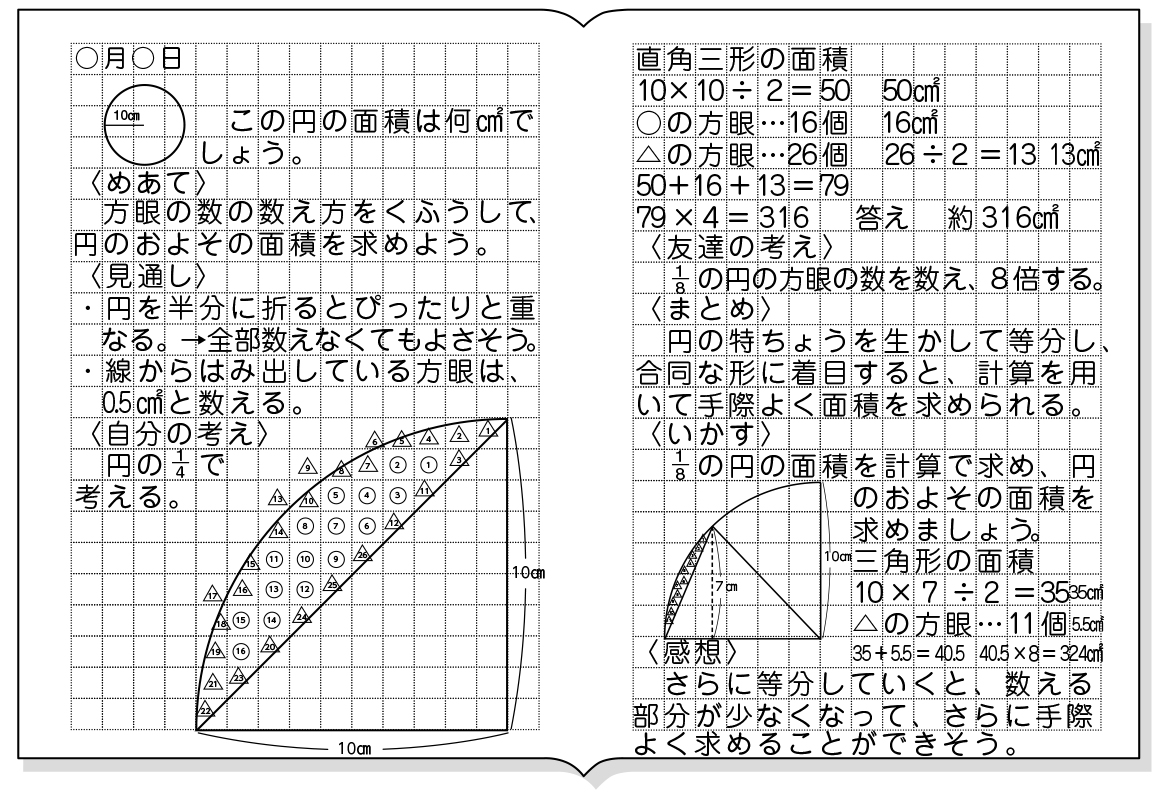



小6算数 円の面積 指導アイデア 1 みんなの教育技術
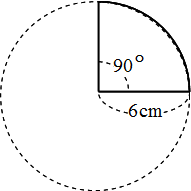



世界一やさしい 円の面積を求める問題の解き方 働きアリ




小6 円 円の面積の求め方 日本語版 Youtube
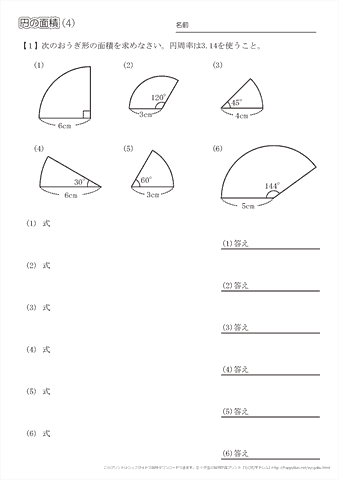



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円 扇形 の面積 周や弧の長さの公式 数学fun
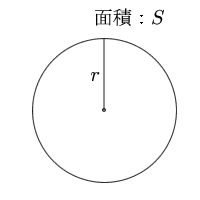



円 面積の計算 計算サイト
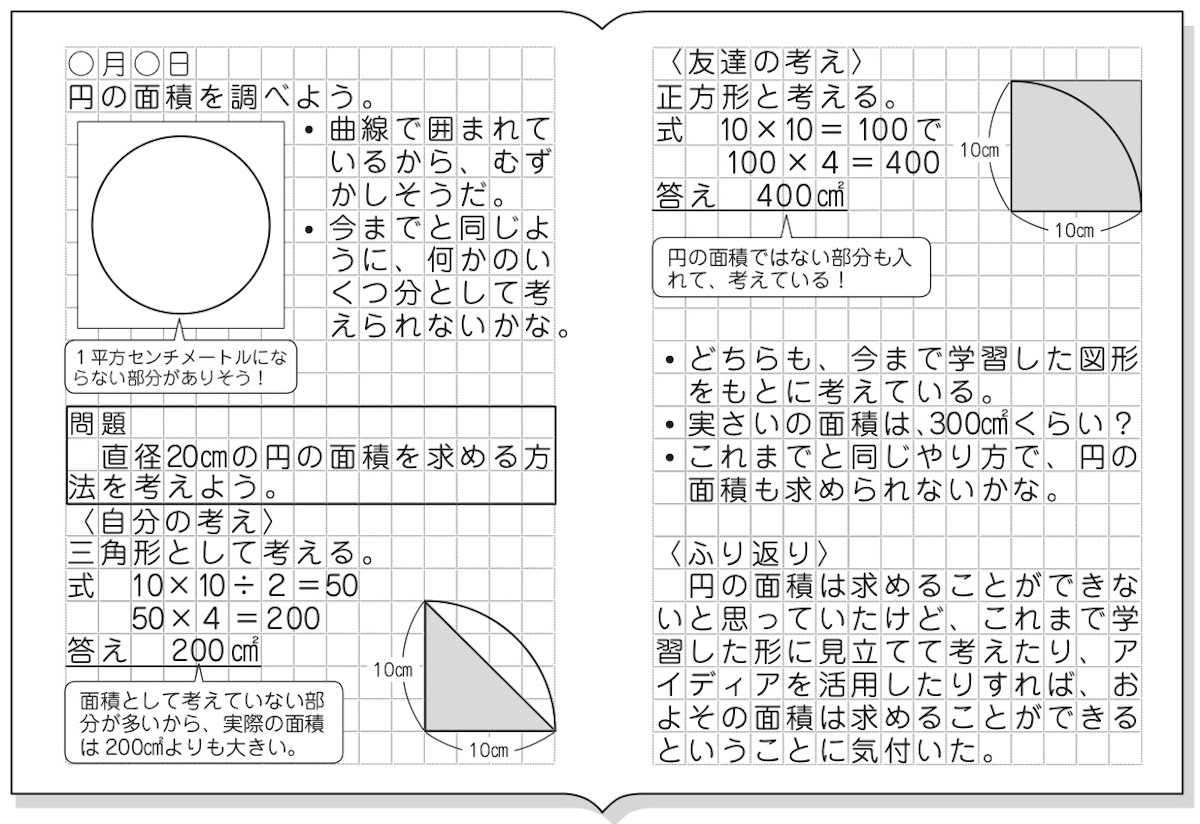



小6算数 円の面積 指導アイデア みんなの教育技術




小6 算数 小6 旧 円の面積 Youtube
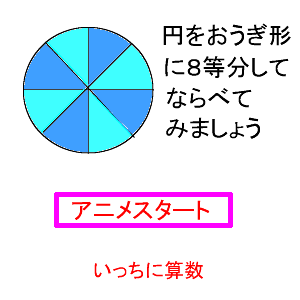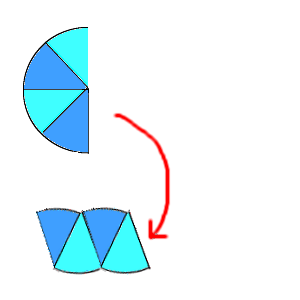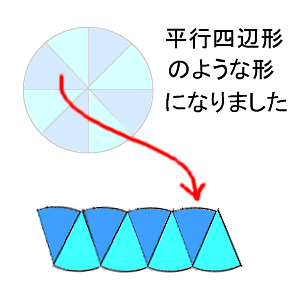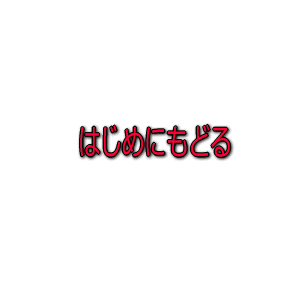



6年算数 円の面積 2 わかる教え方




平成27年度算数教科書読み比べ 8 円の面積の求め方 わさっきhb




円の面積の求め方 公式と計算例



Q Tbn And9gct8mjpenhvsxxfek Ceorhkk1e5jnkqcmelwl1yafnkyt4mflap Usqp Cau
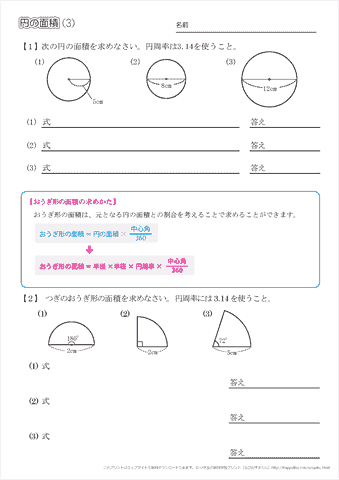



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



面積の考え方 算数の教え上手 学びの場 Com



3
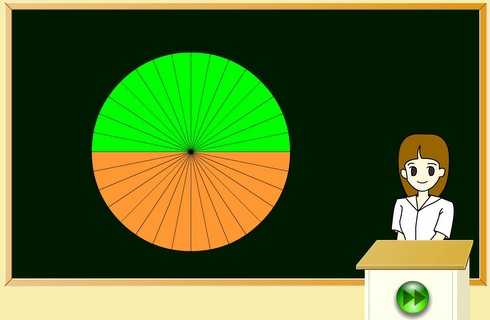



円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ
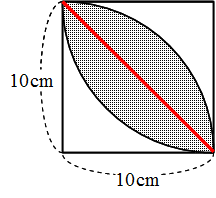



世界一やさしい 円の面積を求める問題の解き方 働きアリ




円の面積の求め方 公式と計算例




スマホok 6年 円の面積 円の面積を求める公式 Youtube
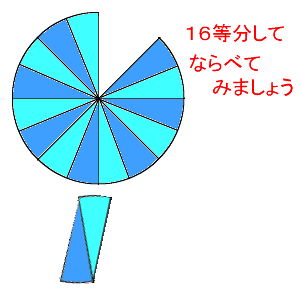



6年算数 円の面積 2 わかる教え方



円の面積の公式 算数の公式
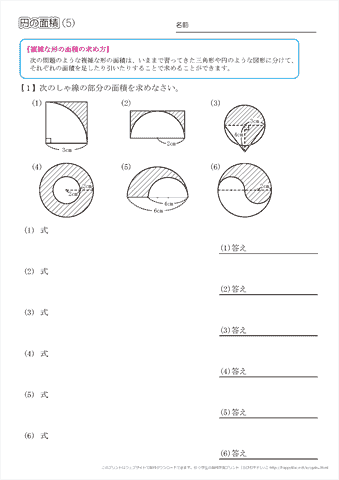



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円の面積がpr 2になる納得の理由 図形を使った証明 数学の面白いこと 役に立つことをまとめたサイト




円の面積の公式 算数の公式



実践記録算数5年



外接円とは 半径の公式や求め方 性質 書き方 受験辞典




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
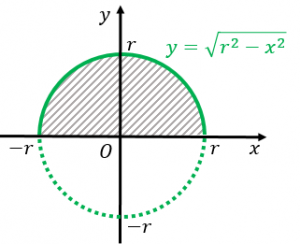



円の面積を積分で計算する2通りの方法 具体例で学ぶ数学




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく



世界一やさしい 円の面積を求める問題の解き方 働きアリ




円の面積 算数用語集



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋
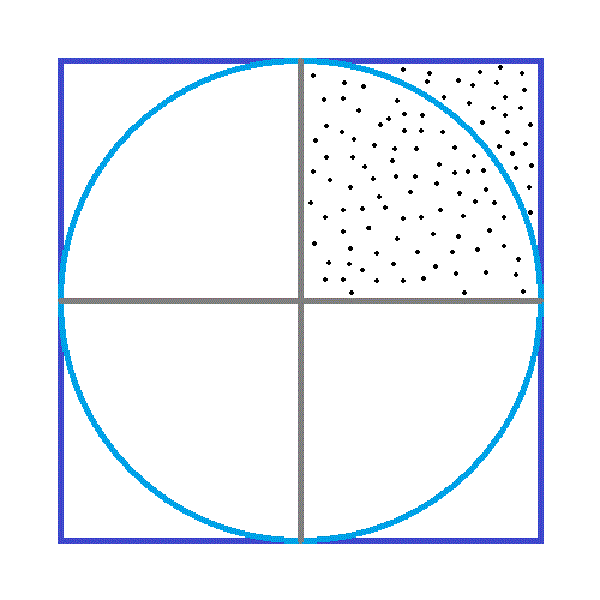



モンテカルロ法による円の面積計算




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



6年算数 円の面積 2 わかる教え方




円の面積の求め方 公式と計算例
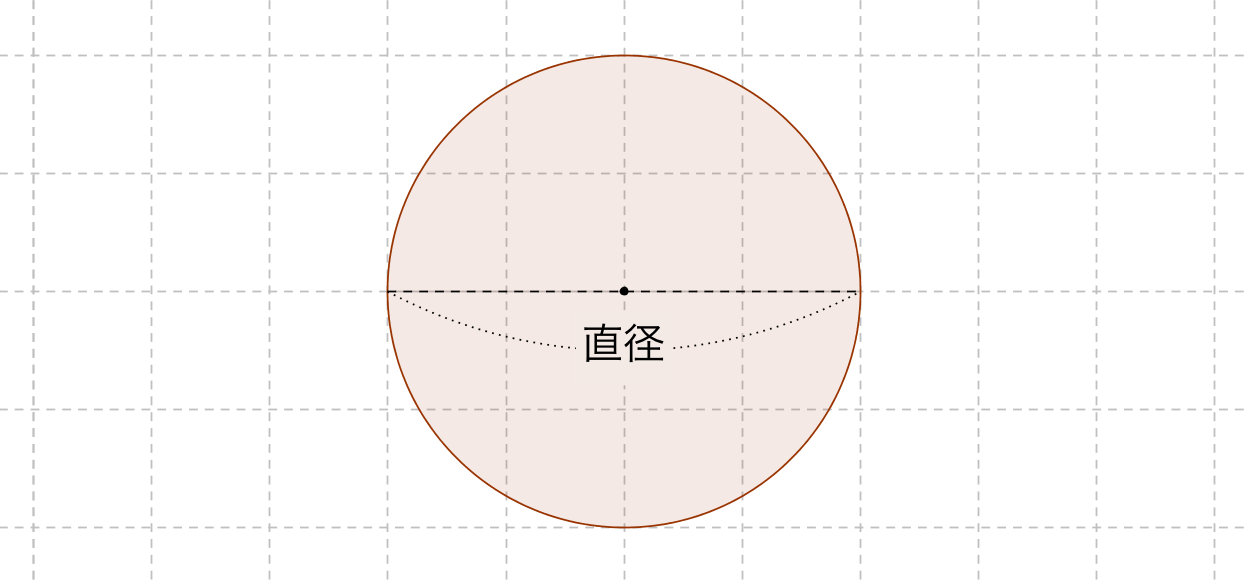



円周の公式 算数の公式



6年算数 円の面積 2 わかる教え方



盲点の英単語 その8 円の面積の求め方を英語で言える 中学の英語をあなどってはいけない



小6算数 円の面積 指導アイデア 1 みんなの教育技術



子供に説明できる 円の面積の公式 の証明 Nikkei Style



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




円の面積 練習応用 Youtube



円の相似を利用した面積の計算 中学受験プロ講師ブログ




面積の求め方 算数の教え上手 学びの場 Com



小6算数 円の面積 指導アイデア みんなの教育技術




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



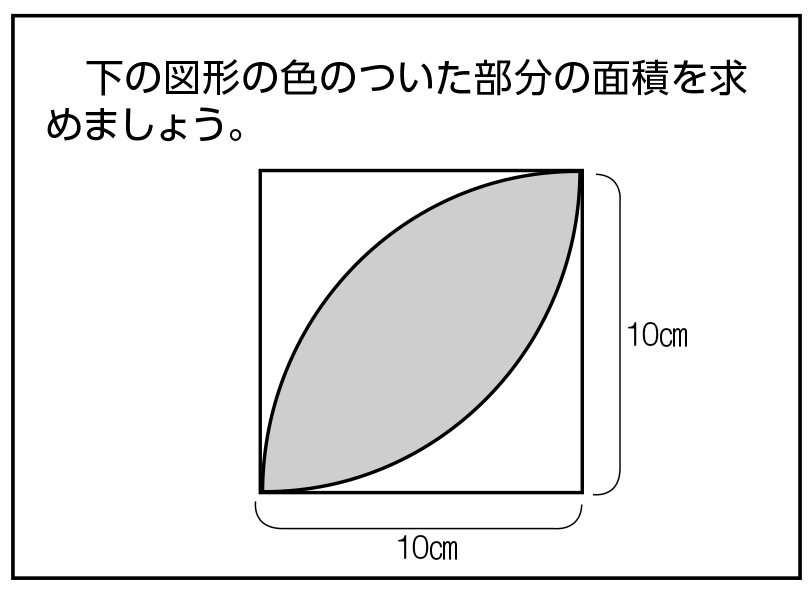
この色の付いた部分の面積の求め方を小学生でも分かるように教えて下さい Yahoo 知恵袋
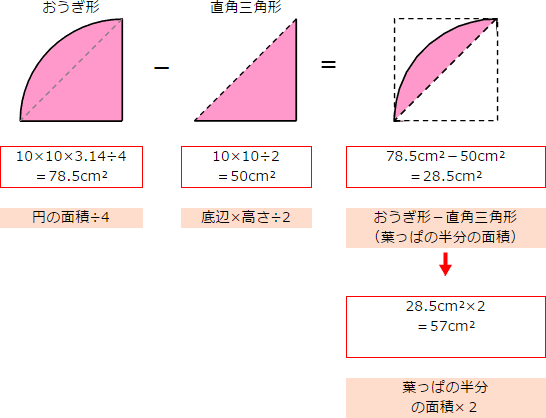



面積の求め方 算数の教え上手 学びの場 Com




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube




円の面積の求め方 公式と計算例



学習教室で Takapの数学日記
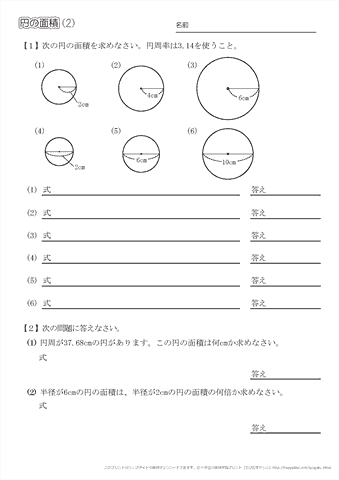



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



0 件のコメント:
コメントを投稿