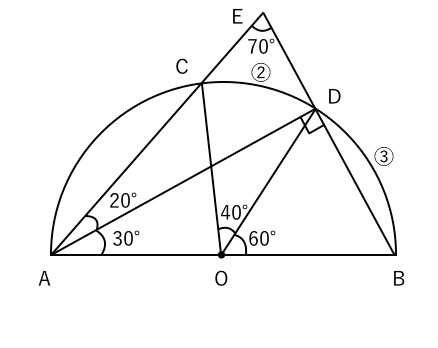
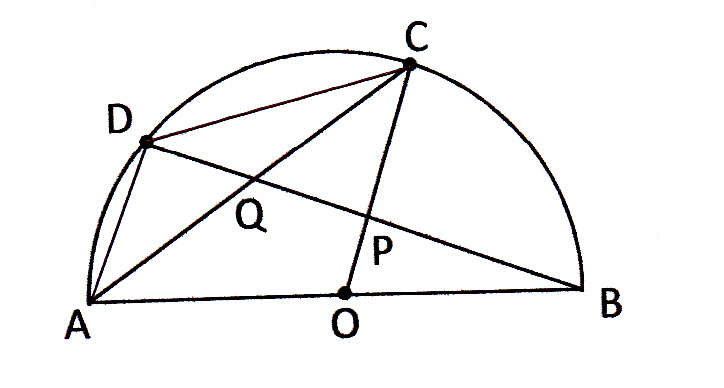
円周角の定理より、 ①,②より、 したがって、 3: x =5:8 x =4.8 ≪答≫ 4.8cm4 直径と円周角の定理を 半円の弧に対する 使って角の大きさを求め 円周角であること たり,図形の性質を証明 に気づき,角の大 したりする。 きさを求めること ができる。 プリント・評テ 5 点がある位置によって 円周角の定理の逆先きほど円周角pabは225°と求めました。 さらに円周角の定理の2番目の「 同じ弧に対する円周角は等しい 」というルールにより、 円周角pab=円周角pcb=225° 線分ocを引くと 円周角の定理の3番目の「 直径に対する円周角は90° 」というルールにより、

中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット
円周角の求め方 中3
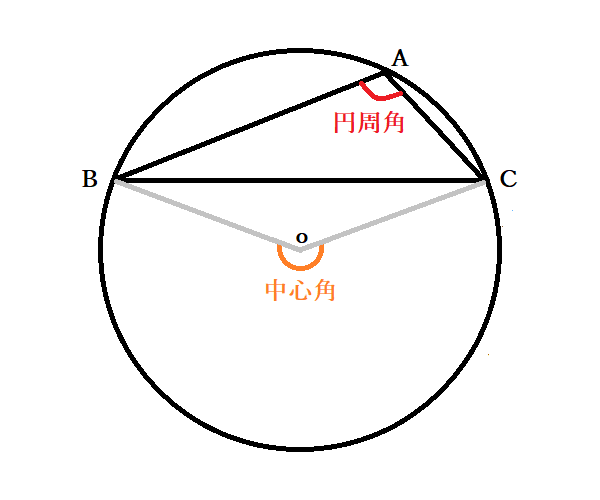
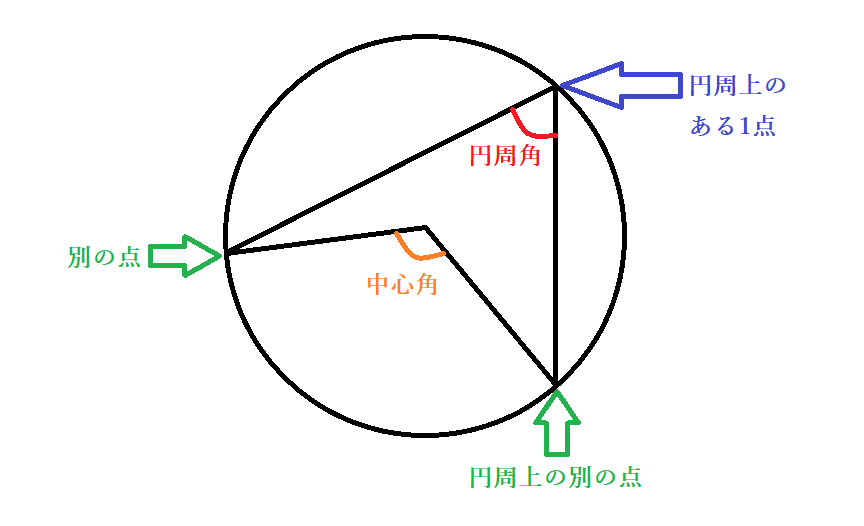
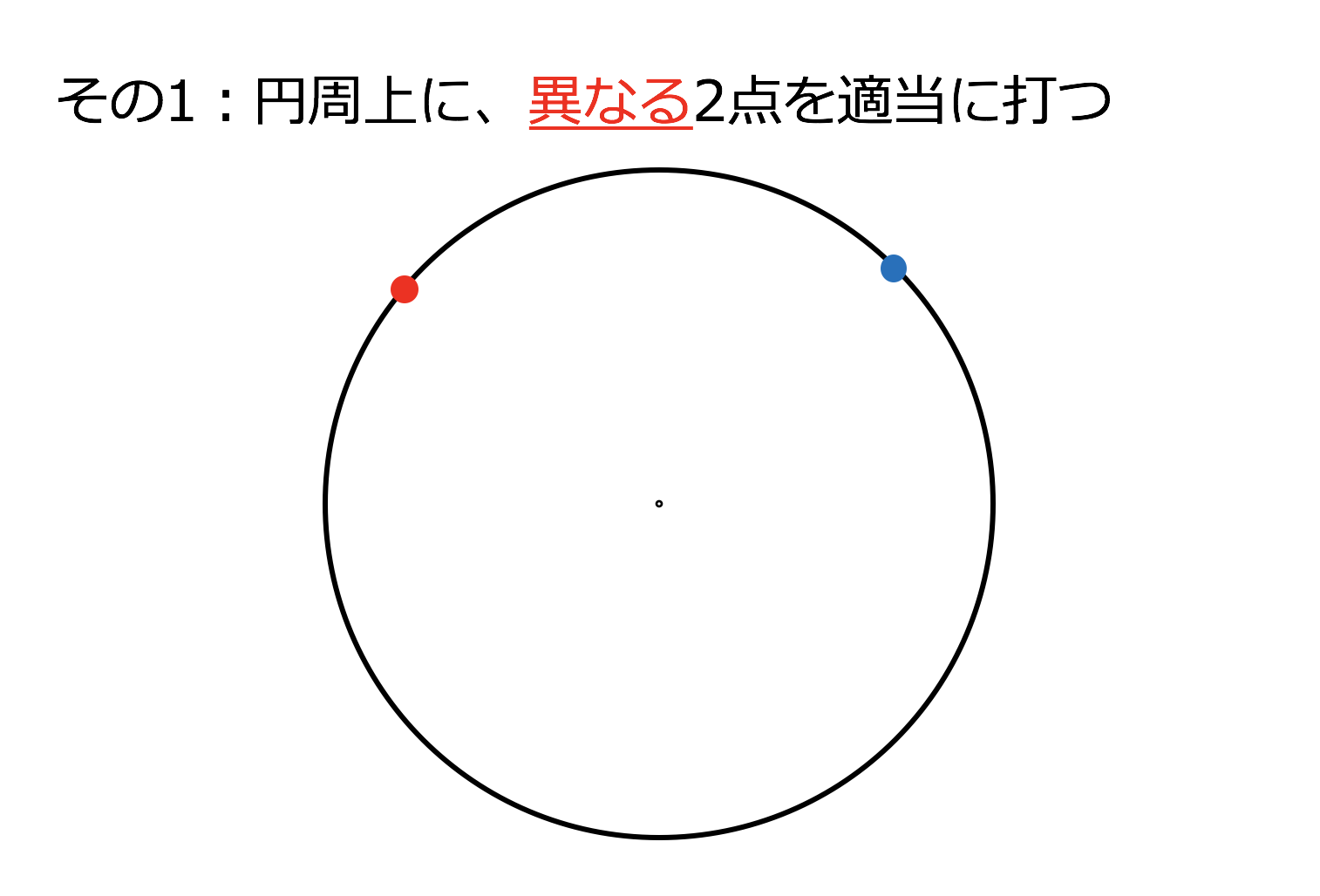
円周角の求め方 中3-正三角形を作図するための考え方 正三角形とは、すべての辺の長さが等しい三角形のことですね。 ということで、 円の中に3辺がすべて等しくなるような三角形を作図したい です。 どのように同じ長さの辺をとるかというと一つの弧に対する「円周角」の大きさは,「中心角」の半分になります. OC=OB= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ B=∠ C (1) ∠ BOA=∠ B∠ C (2) 差で示します. 中心角92°が書いてあって,円周角が書いてないときは,92°÷2= 46° で円周角が求まります.
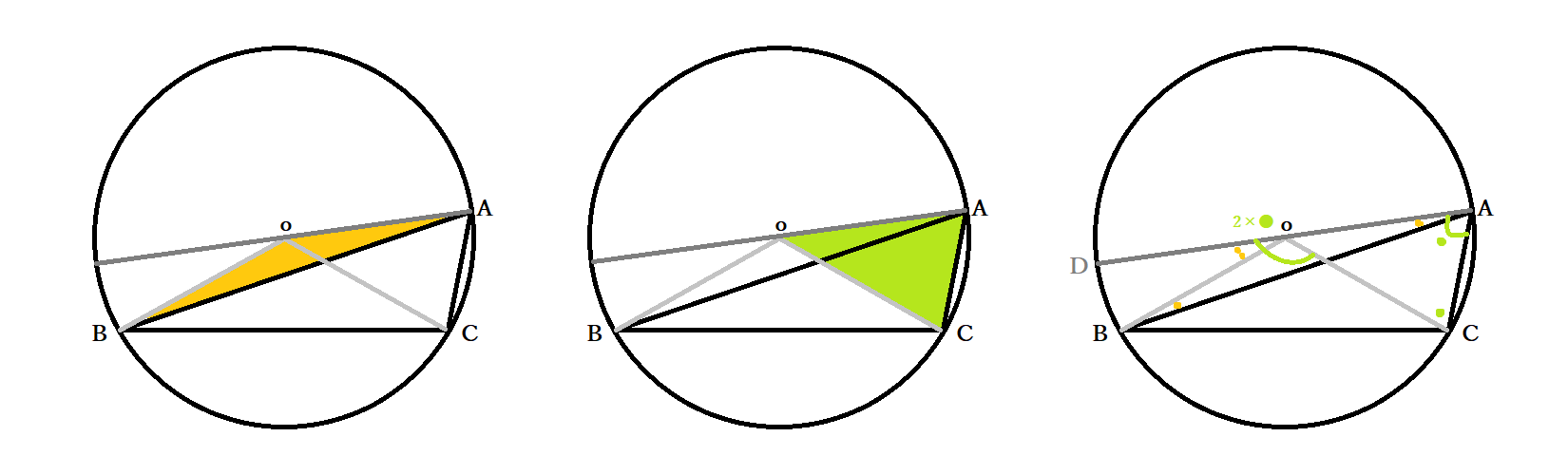



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
第3学年 数学的な見方・考え方を養う「円周角の定理」の授業 また,「主体的・対話的で深い学び」の過程で,ictの活用は効果的で,積極的な利用も求められている。 s1:円の中に四角形ができま円周率は3(えんしゅうりつは3)は、「02年度実施の小学校 学習指導要領の改訂にともなって、日本の算数教育にてそれまで314と教えていた円周率の近似値を3 と教えることになった」という内容が世間に広まった事象である。 実際にはこれは事実ではなく、改訂後も円周率の近似値は314でとなり,18mになる。正三角形は3つの辺の長さが等しいので, 円の半径にあたる辺ACも18mになる。 円周は,直径×円周率で求められるから,この円の円周は, となり,mになる。 解答のポイント! 6つの三角形はどれも合同な正三角形であること
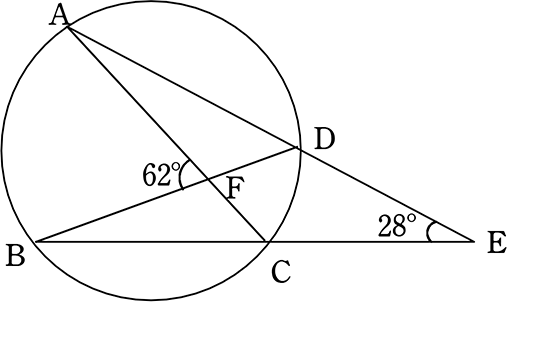
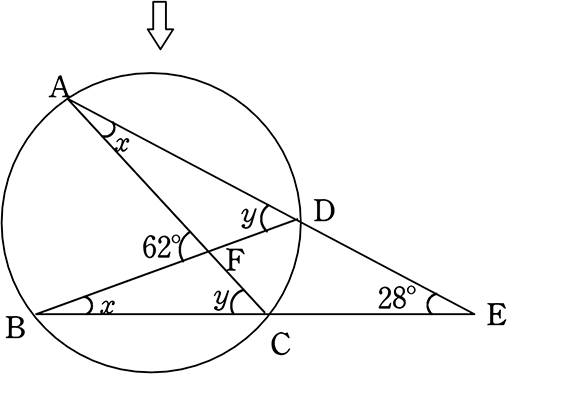
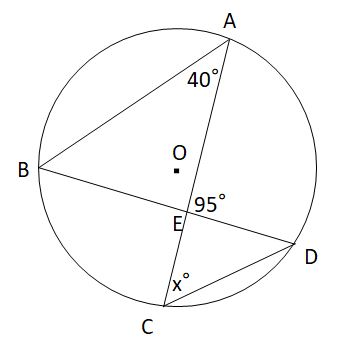
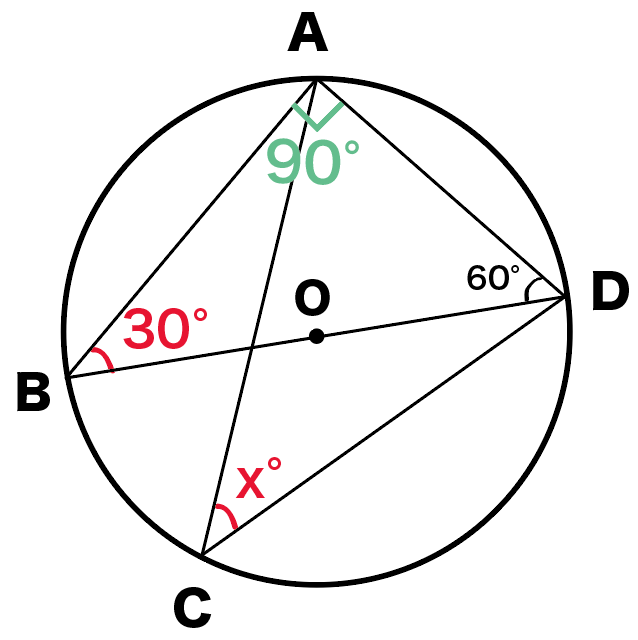
∠badは半円の弧に対する円周角なので、 ∠bad=90° ∠bac=∠bad∠cad=90°62°=28° ∠\(x\)と∠bacはともに弧bcの円周角なので、 ∠\(x\)=∠bac= 28° 円周角の問題を解くコツ についてまとめます。 3つのポイントに 注意して問題に取り組むこと。 1.弧に注目する 2.直径が出てきたら 90°の円周角を探す 3.補助線を引いてみる 「できる」と自分を信じて 中3 中3 数学 円周角の定理 中学生 数学のノート Clear 表紙 1 公開日時 年08月11日 00時31分 更新日時 21年02月18日 23時51分 中学生 3年生 数学 円周角の定理 (円周角と中心角)
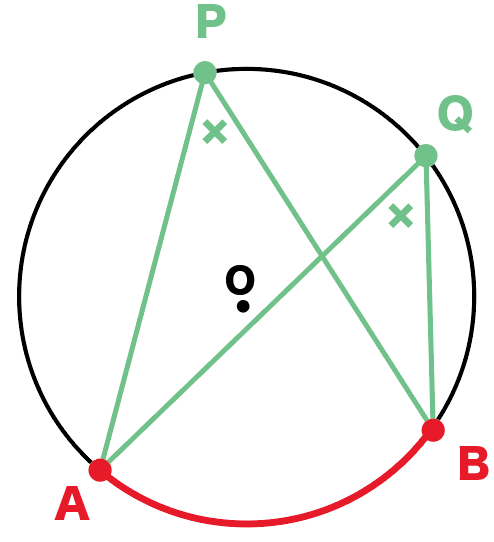
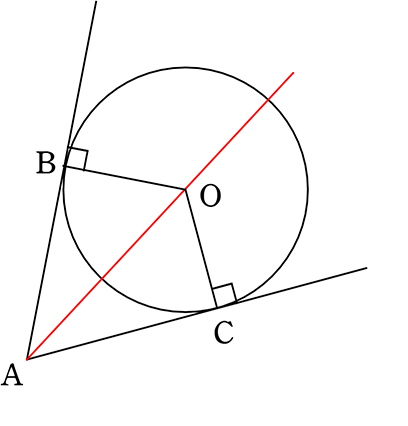
円周角3 図で、abは円oの接線である。cが接点、oが中心であり、eとdは円周上にある。 a b c d e o (1) ∠ocbは何度か。 (2) ∠dcb=40簡単なので、しっかり確認しましょう。 定理 1 : 1 つの弧に対する円周角は中心角の半分 定理 2 : 1 つの弧に対する円周角はすべて等しい ∠ A Q B = ∠ A P B = ∠ A R B (すべて AB ⌢ に対する円周角) 1:10 例題 10 選 (1) 対頂角は等しい (紫の角) 1 つの弧中2数学 中2数学平行四辺形の3つの性質 中3数学 円の性質円周角の角度の求め方の3つのパターン 中2数学 数学の証明問題の解き方がわかる4つのステップ 中2数学 162 コンパスで作図




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
ビデオ 数学中356 円周角の定理①(基本編) 21, 八月 円の2つの点を結んでその中心を通る線分は、自己交差を持たない閉じた線と一定の関係にあり、そのすべての点は中心から同じ距離にあります。 円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを 中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It 3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しTitle FdData中間期末過去問題中学数学3年(円周角と中心角/円周角の定理/接線) Author Fd教材開発 Created Date
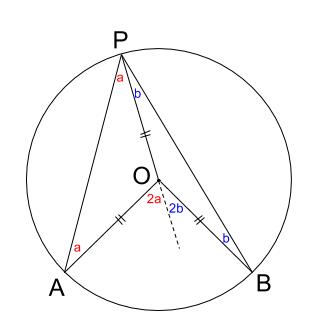



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




10月1日更新 半円を弧にする円周角についての証明 成績 上がってます 根城学習塾 八戸市
3連休最終日。 中3のテスト対策授業もこれが最後です。 最後に行うのは円周角の定理の解説授業です。 普通の問題はある程度演習してもらえているので、この授業では特に注意すべき問題をピックアップして解説しました。 円周角の定理とは まず、問題を解いていく上で知っておいて欲しい知識がこちら 同じ弧に対する円周角の大きさは等しい 同じ弧に対する中心角の大きさは円周角の大きさの2倍 直径に対する円周角は90° 弧の長さが等しければ、円周角・中心角の大きさは等しい 同じ弧でなくても長さが等しければ、円周角、中心角は等しくなります。 円周角、中心角の大きさは円周角は中心角の半分 同じ弧に対する、 円周角は中心角の半分 だよ。 すると、図の角度が分かるね。 ここから、三角形の 外角の定理 を使うと、 ∠x+50°=100° となるよ。 ちなみに、この三角形の 2辺は円の半径 でできている、つまり 二等辺三角形 になっていることから、答えを求めることもできるよ。 (1)の答え




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
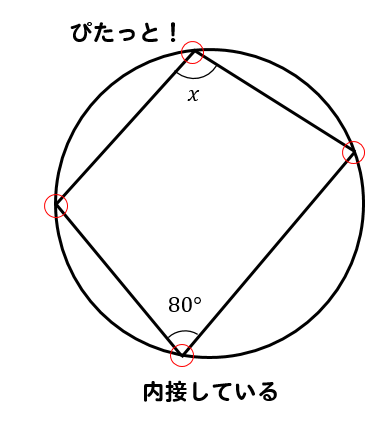



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
→ ∠b = ∠b' (円周角の定理) → ∠a = 90° (bcが直径 ⇔ ( ならば ) 円周角は90°) ・三角形の「内角」から見て = 180°90° → = 180°90° ・「直線(直径を延長した直線)」b'm から見て = 180°90° → = 180°90° → どちらも 180°90° ∴ = たとえば、半径3cmで中心角1度の円の面積を求めなさいという問題が出題されたとします。 円周率=314で考えましょう。 この円全体の面積は 円の面積=半径×半径×円周率で導き出せます。 円の面積=3×3×314 つまり26㎠です。 扇形の面積はこの円の1上のような円があったとします。 大きさは何でもいいです。 この円の上に点を3つ乗せていくと、 このようになります。 点はそれぞれ、点A,点B,点Cとしておきます。 次に、乗せた3つの点の2つの線分でつないでいきます。 こうすると、線分と線分に挟まれた点Bのところに、角が出来ていることが分かります。 この角を、線分を構成するA,B,Cを用いて∠ABCと表せ




世界一わかりやすい数学問題集中3 6章 円の性質
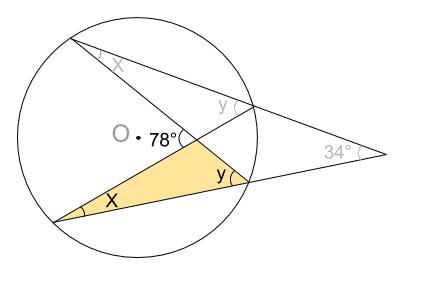



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su
2数 いろいろな角の求め方円周角 補助線を引く問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 2つの半径OA, OBと弦ABによって できる三角形は必ず二等辺三角形になる。 A B O 中心Oに向かって補助線をひき、二等辺三角形や数学Ⅰ 三角比と図形③ 四角形の面積の求め方 ;




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



1
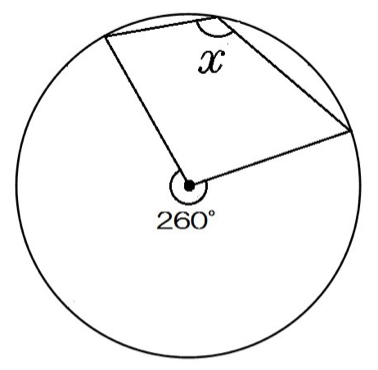
商を求めてから 約分する。 = 3 7 (考え方2) 6 7 ÷2= 6 3 7×2 1 ⇦ 計算の途 と 中 ちゅう で 約分する。 = 3 どちらの考え方で計算しても答えは同じになりますが,(考え方2)のように,計算の途中 で約分するほうが,簡 かん 単 たん に計算できますあとは、 「円周角は中心角の半分」 といった性質から、この四角形の内角を求めていくと、 これら、内角をすべてたすと、360°になるね。 (3)の答え同じ弧に対する中心角は、円周角の \(2\) 倍の大きさなので、下図のようになります。 \(=502x\) より、\(x=15°\) と求まります。



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu
中3 中3〜円周角の定理・円の性質の利用〜 中学生 数学のノート Clear 表紙 1 2 3 公開日時 17年01月23日 時34分 更新日時 年06月25日 時46分 中学生 3年生(2)円周角と中心角の関係や 、 同じ弧に対する円周角の性質を見い出すことができる。 数学的な見方や考え方 (3) 円周角と中心角の関係や同じ弧に対する円周角の性質などを記号を用いて表したり、その意味 を読み取ったりすることができる。 今日は、 テストにでやすい円周角の求め方 を3パターン紹介していくぞ。 円周角の定理を使うだけの問題;




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear




Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
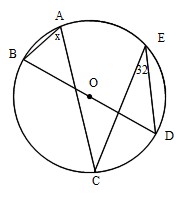
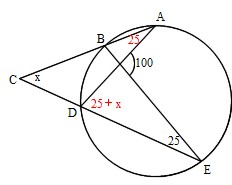
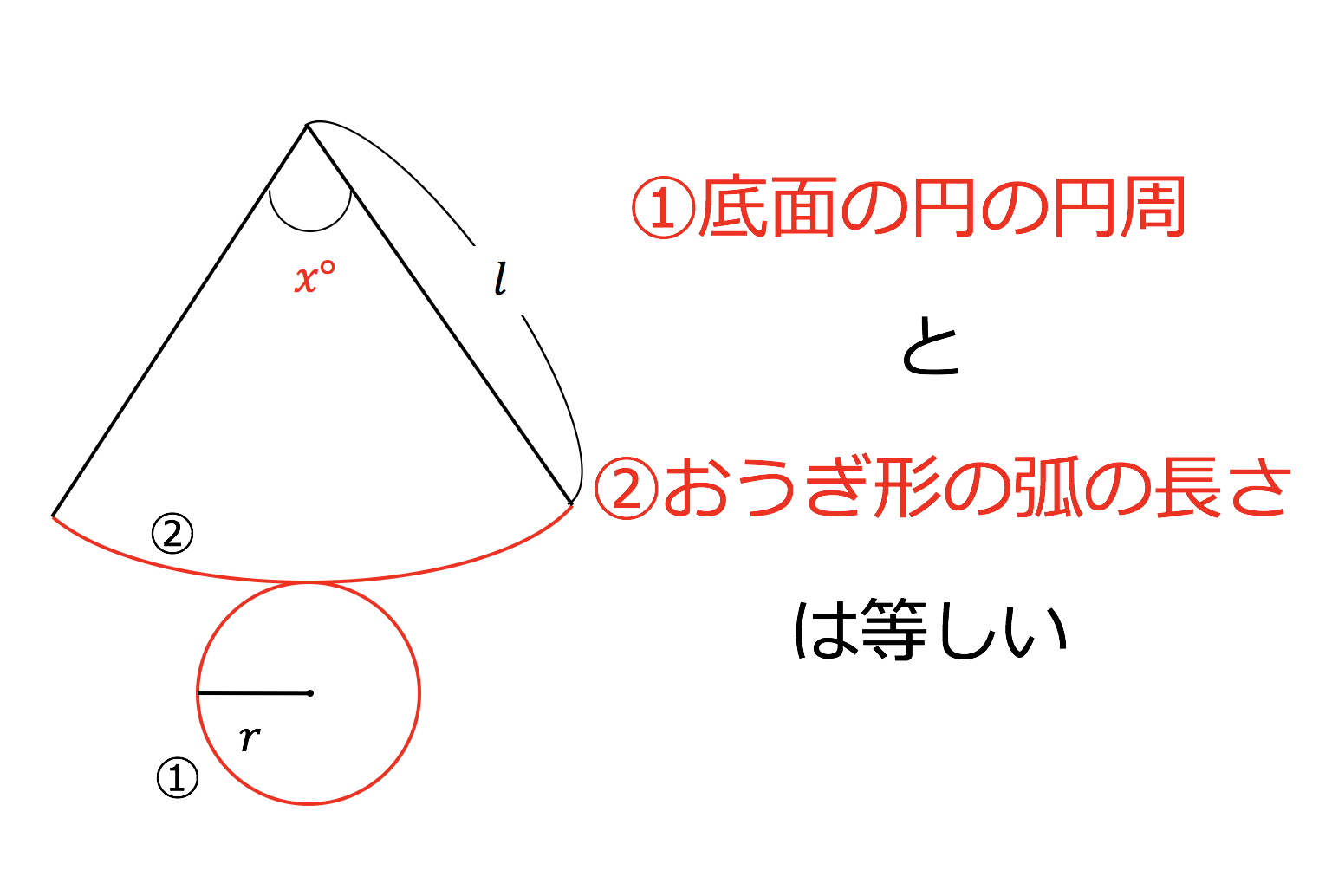
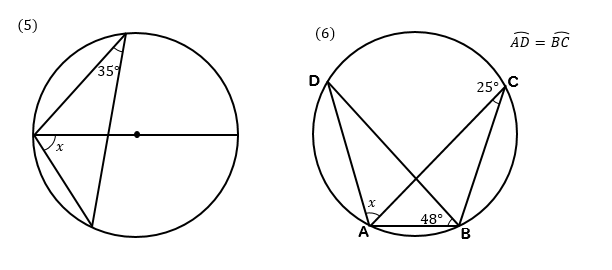
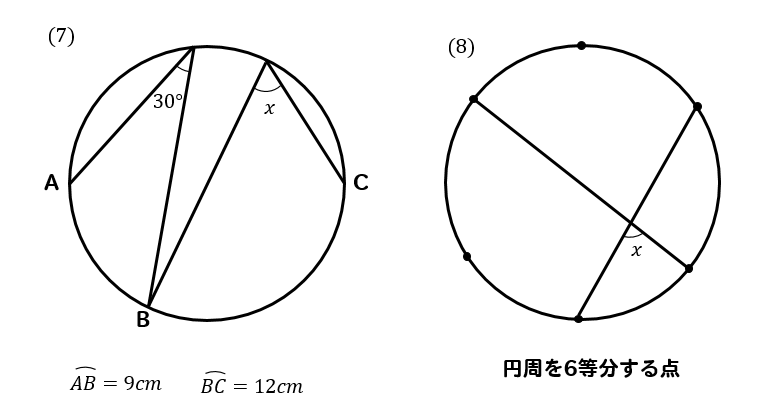
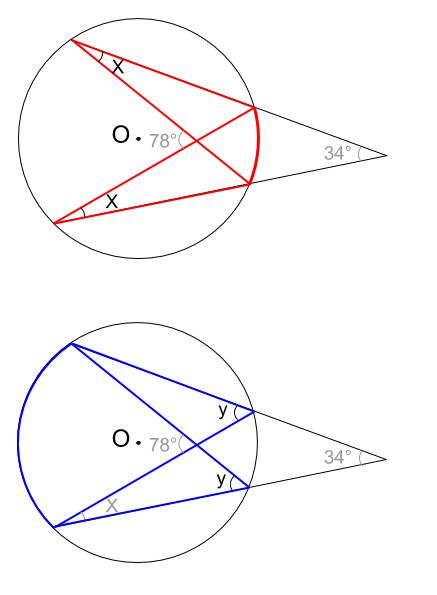
円の性質円周角の角度の求め方の3つのパターン Qikeru 円周角の角度の求め方は3パターン?? やあ,Drリードだぞいっ!! 円周角の定理は頭に入ったよな! だよな!円周角の定理とはなんだろう?!?やあ、ぺーたーだよ。 中3数学もいよいよ大詰め。∠xは CD に対する円周角、∠ADBは AB に対する円周角である。 弧の長さは円周角の大きさと比例するので x∠ADB=25 ∠ADB= 5 2 x ≫ ∠ADBは EDBの外角となっている。 三角形の外角はそれと隣り合わない2つの内角の和に等しいから ∠ADB=∠DEB∠DBE ≫ 5 2 x=24°x 3 2 x半径 $3 \rm cm$ の円なので、$2×3×π=\textcolor{red}{6π\rm cm}$ 問題側面のおうぎ形の中心角の大きさを求めなさい。 側面のおうぎ形は半径 $5 \rm cm$ の 円の一部 といえます。よって、 円周と弧の長さの比率 から、おうぎ形の中心角を求めることができます。




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



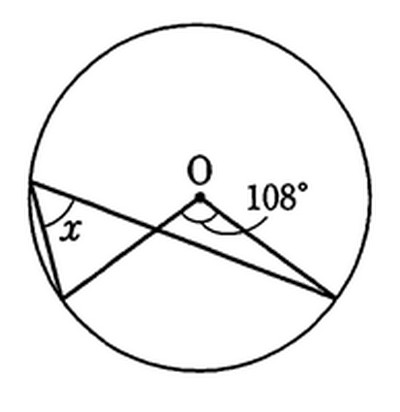
中3数学角度円周角 下の写真のxの求め方を分かりやすく教えて頂きたいです Yahoo 知恵袋
中2数学 平行線と角 角度の求め方 ; 中3数学円周角の定理円周角と中心角まとめと問題 円周角と中心角(円周角の定理)に関するまとめと問題です。 円周角と中心角の関係がわかっていても解きづらいこともありますよね。 基本問題の中から質問の多い問題と、問題の解き方も簡単に解説してますので、円周角が苦手という人は参考にしてください。 変更をプレビュー 1 円周角と中心角まずは、 「円周角は、中心角の半分」 。円の角度の、最も基本的な性質だね。 円の角度の、最も基本的な性質だね。 それに関連して、 「直径の円周角は、つねに90°」 。




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生
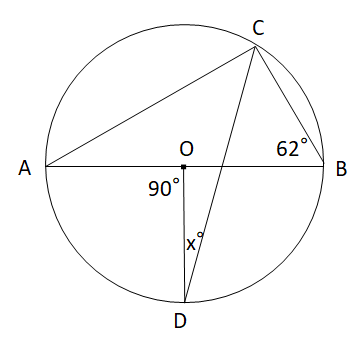
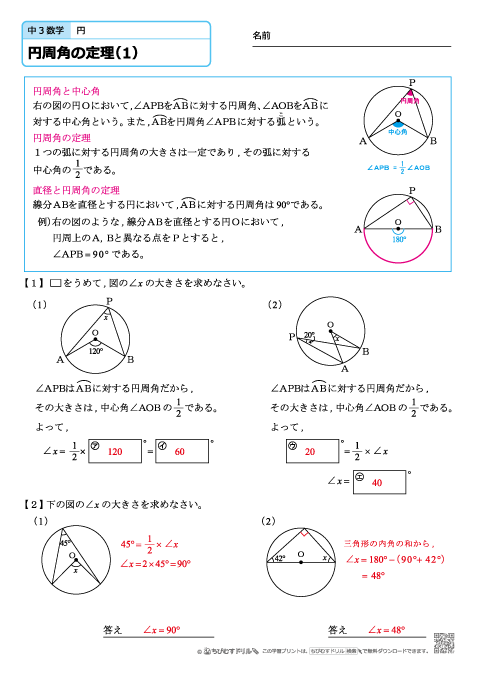
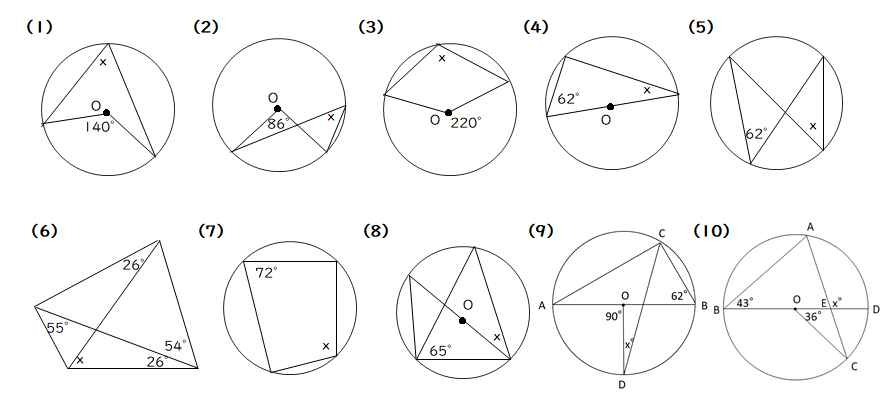
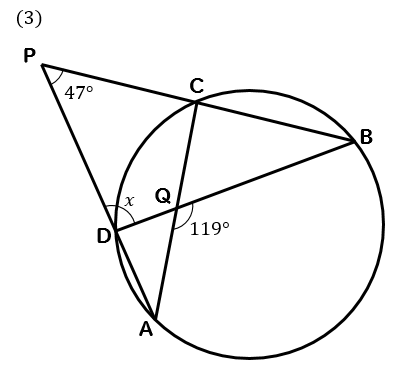
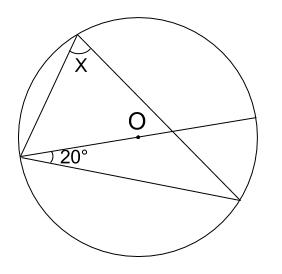
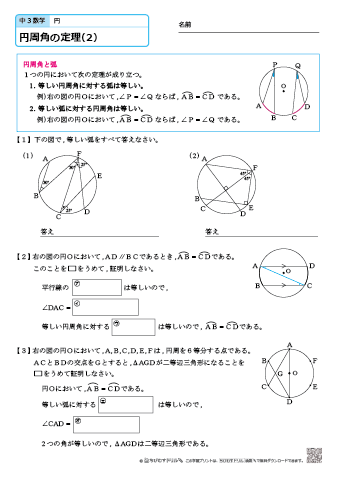
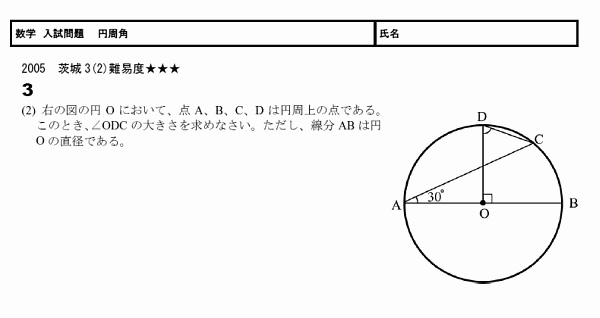
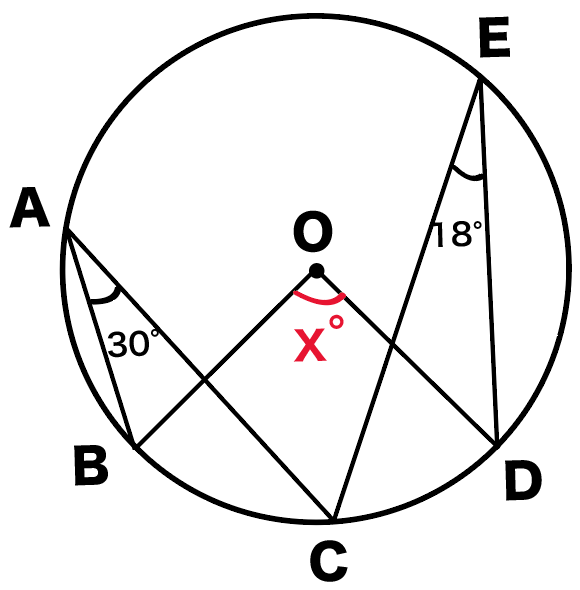
X ,∠y の大きさを求めたい。 にあてはまることばや数を答えなさい。 (1) BCに対する円周角である。 ∠ x は BC に対する中心角だから,∠ x = ① ° OBC は OB=OC の ② 三角形だから, ∠ y = ③ ° 答え ① ② ③ 答え ① ② ③ ④ (3) AQBに対する ① である。 円周角より,その弧に 円周角の定理は 「円周角=½ 中心角」ですから、 ∠bac=½ ∠boc を示せばいいわけです。 oからbに補助線を引いて、大きさが同じ角に印をつけてみましょう。 注意すべきなのは、oは円の中心であり、a,b円周上の点であるため、oa=obであることです。円周角は中心角の半分(中心角は円周角の2倍)だから x=2× (31°17°)=96° (答)



円と三角形 角度 中学から数学だいすき



中3円周角の問題です Xとyの角度の求め方を教えてくださ Yahoo 知恵袋




中3数学 円周角 ブーメラン型四角形 まとめと問題




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット




数学 中3 57 円周角の定理 少し応用編 Youtube



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中3 数学 円4 角度の求め方 15分 Youtube




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学




円周角の定理の基本 計算 無料で使える中学学習プリント




高校数学a 共円条件 4点が同一円周上にある条件 受験の月




円 扇形 の面積 周や弧の長さの公式 数学fun




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4



中学数学 円周角 中心角




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu



円周角




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく




円周角の定理 中学校学習指導要領および教科書の扱い 身勝手な主張




中3数学 円周角の定理 勉強 Youtube スタディチューブ



中学数学 円周角 中心角



中3数学 円周角の定理を使った定期テスト予想問題 Pikuu



円周角



7f0kbv Ki Gytm




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円周角の定理は人生の縮図 円周角の定理が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦
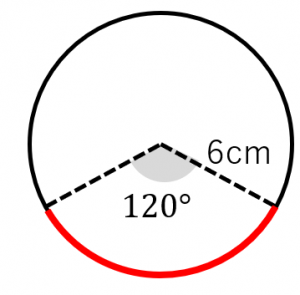



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
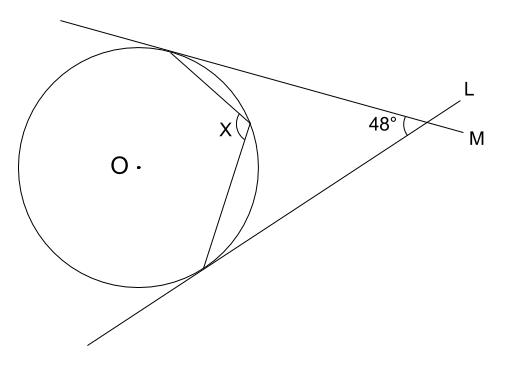



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



1



1




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




中3 数学応用 円周角の定理 証明 中学生 数学のノート Clear




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
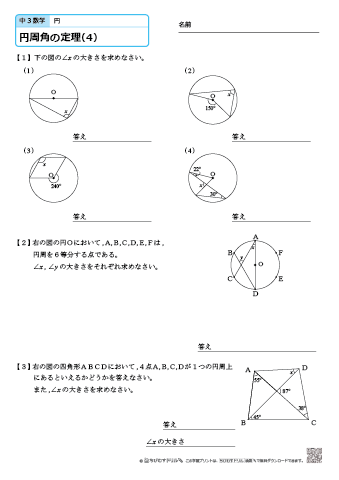



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



中学数学 円周角 中心角




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



円周角と比の問題 苦手な数学を簡単に



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



円周角の定理とその逆の証明 高校数学マスター



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su



1



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog




円周角 三角形の外角の関係を使う問題



中学 数学 問題 無料学習プリント教材




中学数学 円周角 中心角



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方




円周角の定理の基本 計算 無料で使える中学学習プリント




の求め方を教えて下さい 一問だけでも大丈夫です Clear



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




中学3年の数学 動画 円周角の定理 少し応用編の問題 19ch



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生




数学 中3 56 円周角の定理 基本編 Youtube




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




中3数学 円周角 ブーメラン型四角形 まとめと問題




中学3年数学 円周角の定理 計算 証明問題 3学期期末テスト 赤城 ᐡᐤᐡ



円周角の定理と中心角 中学3年数学 Youtube




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
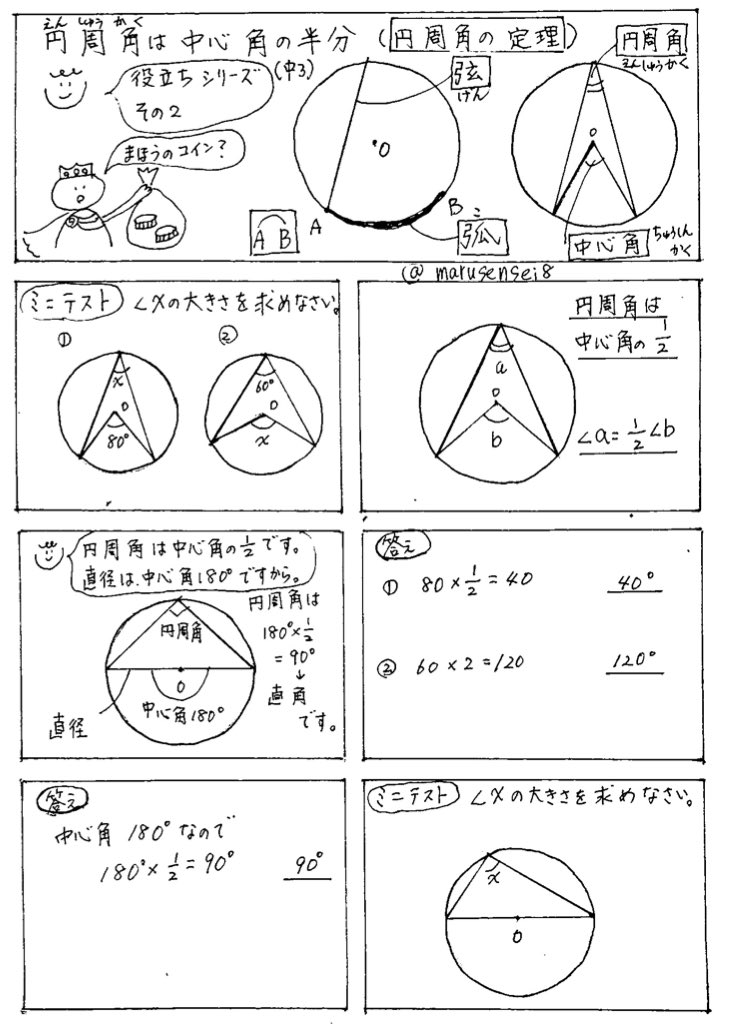



円周角の定理




中3数学 円周角の定理 Examee
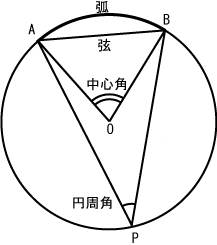



円 数学 Wikiwand




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest
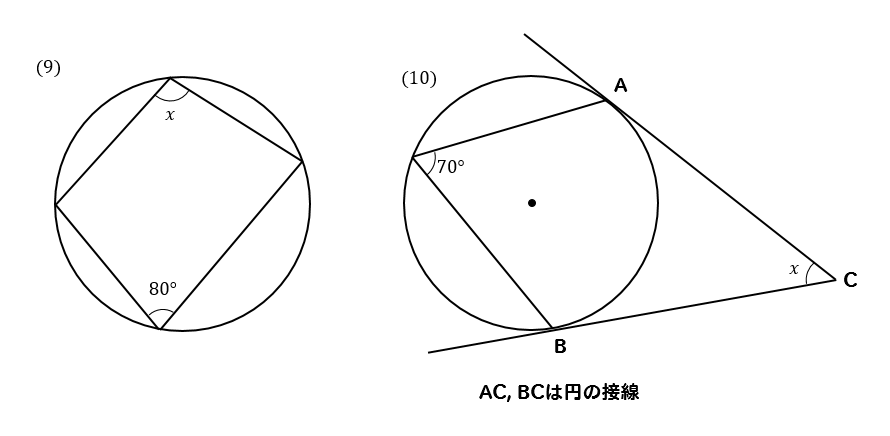



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
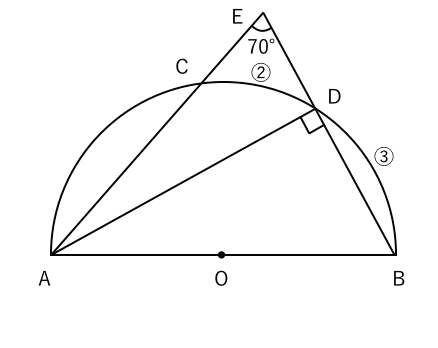



円周角と比の問題 苦手な数学を簡単に



0 件のコメント:
コメントを投稿